Cho tứ giác ABCD.Kẻ đường chéo BD từ C vẽ 1 đường thẳng song song BD.Cắt AD kéo dài ở E.Nối B với E.So sánh dt ABE và ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 12 2018
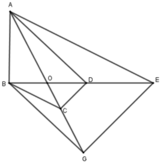
Theo định lý Ta-lét:
Ta có: AE // BC nên O E O B = O A O C (1) hay A đúng.
BG // AD nên O B O D = O G O A (2) hay C đúng
Từ (1) và (2) suy ra: O E O B . O B O D = O A O C . O G O A hay O E O D = O G O C , do đó EG // CD (định lí Talet đảo) hay D đúng
Vậy B sai
Đáp án: B
9 tháng 6 2019
a.
Theo định lý Thales,ta có:
\(OE//BC\) nên \(\frac{AE}{EB}=\frac{AO}{OC}\left(1\right)\)
\(OF//CD\) nên \(\frac{AF}{FD}=\frac{AO}{OC}\left(2\right)\)
Từ (1);(2) suy ra \(\frac{AE}{EB}=\frac{AF}{FD}\Rightarrow FE//BD\) theo ĐL Thales đảo.
b.
Theo định lý Thales,ta có:
\(OG//AB\) nên \(\frac{AO}{OC}=\frac{BG}{GC}\left(3\right)\)
\(OH//AD\) nên \(\frac{AO}{OC}=\frac{DH}{HC}\left(4\right)\)
Từ (3);(4) suy ra:\(\frac{BG}{GC}=\frac{DH}{HC}\Rightarrow BG\cdot CH=CG\cdot DH\left(đpcm\right)\)