Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AB=a, BC=2a, AA'=3a. Một mp (P) đi qua A và vuông góc với A'C lần lượt cắt các đoạn CC', BB' tại M,N.
a, VC.A'AB
b, Chứng minh: \(AN\perp A'B\)
c, VA'AMN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

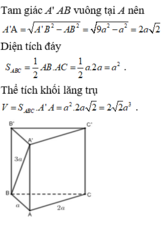
Chọn A.
Phương pháp
Tính diện tích tam giác đáy và chiều cao lăng trụ suy ra thể tích theo công thức V=Bh .
Cách giải:

Chọn C
Gọi h là độ dài cạnh bên của lăng trụ đứng đã cho.
Vì MNPQ là tứ diện đều nên
![]()
![]()
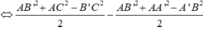 = 0
= 0
![]()
![]()
![]()
*Chú ý một khối tứ diện đều (tất cả các cạnh bằng nhau) hoặc một khối tứ diện gần đều (độ dài cặp cạnh đối bằng nhau) thì cặp cạnh đối của chúng vuông góc với nhau (xem chương góc và khoảng cách).
*Chú ý tích vô hướng cho hai véctơ cùng gốc
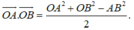
a.
\(\left\{{}\begin{matrix}BB'\perp\left(ABC\right)\Rightarrow BB'\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ABB'A'\right)\)
\(\Rightarrow BC=d\left(C;\left(A'AB\right)\right)\)
\(S_{A'AB}=\dfrac{1}{2}S_{ABB'A'}=\dfrac{3a^2}{2}\)
\(\Rightarrow V_{C.A'AB}=\dfrac{1}{3}BC.S_{A'AB}=\dfrac{1}{3}.2a.\dfrac{3a^2}{2}=a^3\)
b.
Theo cmt, \(BC\perp\left(ABB'A'\right)\Rightarrow BC\perp AN\)
Mà \(\left\{{}\begin{matrix}A'C\perp\left(P\right)\\AN\in\left(P\right)\end{matrix}\right.\) \(\Rightarrow AN\perp A'C\)
\(\Rightarrow AN\perp\left(A'BC\right)\Rightarrow AN\perp A'B\)
c.
Ta có: \(AA'||BB'\Rightarrow d\left(B;AA'\right)=d\left(N;AA'\right)\)
\(\Rightarrow S_{A'AN}=S_{A'AB}\)
Lại có: \(CC'||BB'\Rightarrow CC'||\left(ABB'A'\right)\)
\(\Rightarrow d\left(C';\left(ABB'A'\right)\right)=d\left(M;\left(ABB'A'\right)\right)\)
\(\Rightarrow V_{A'AMN}=V_{CA'AB}=a^3\)