GIÚP EM VÓI Ạ,EM CẦN GẤPPPPPP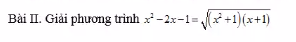
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
1) \(\Rightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
2) \(\Rightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
3) \(\Rightarrow\left(4x-3\right)\left(7-12x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=\dfrac{7}{12}\end{matrix}\right.\)
4) \(\Rightarrow x^3+8-x^3+25x=-17\)
\(\Rightarrow25x=-25\Rightarrow x=-1\)
5) \(\Rightarrow\left(3x-2\right)\left(3x+2\right)-2\left(3x-2\right)^2=0\)
\(\Rightarrow\left(3x-2\right)\left(3x+2-6x+4\right)=0\)
\(\Rightarrow\left(3x-2\right)\left(-3x+6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=2\end{matrix}\right.\)
Bài 3:
c: \(x^2+7x+12=\left(x+3\right)\left(x+4\right)\)
d: \(x^3-7x-6\)
\(=x\left(x-1\right)\left(x+1\right)-6\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-x-6\right)\)
\(=\left(x+1\right)\left(x-3\right)\left(x+2\right)\)




R=1/2CD=a
h=AD=2a
S1=Sxq=2*pi*r*h=2*pi*a*2a=4*pi*a^2
S2=Stp=2*pi*r^2+2*pi*r*h
=2*pi*a^2+2*pi*a*2a
=6*pi*a^2
>S1/S2=2/3


\(S_{Xq}=2\cdot pi\cdot2^2+\dfrac{1}{2}\cdot\sqrt{5}\cdot2=3\sqrt{5}\cdot pi\)
 giúp em bài 1 dạng 3 vói em, em cần gấp lắm, em cảm ơn ạ
giúp em bài 1 dạng 3 vói em, em cần gấp lắm, em cảm ơn ạ






ĐK : x \(\ge-1\)
Ta có : \(x^2-2x-1=\sqrt{\left(x^2+1\right)\left(x+1\right)}\)
<=> \(\left(x^2+1\right)-2\left(x+1\right)=\sqrt{\left(x^2+1\right)\left(x+1\right)}\)
Đặt \(\sqrt{x^2+1}=a;\sqrt{x+1}=b\)(\(a>0;b\ge0\))
Khi đó a2 - 2b2 = ab
<=> (a - 2b)(a + b) = 0
<=> a - 2b = 0
<=> a = 2b
<=> \(\sqrt{x^2+1}=2\sqrt{x+1}\)
<=> \(\left\{{}\begin{matrix}x^2+1=4x+4\\x\ge-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-4x-3=0\\x\ge-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=\sqrt{7}+2\\x=-\sqrt{7}+2\end{matrix}\right.\\x\ge-1\end{matrix}\right.\Leftrightarrow x=\sqrt{7}+2\)