Ba đội công nhân cùng làm việc. Trong một giờ đội thứ nhất là được 2 9 công việc, đội thứ hai là được 1 3 công việc, đội thứ ba làm được 5 27 công việc. a) Theo em trong một giờ đội nào làm được khối...

HP

huy phạm

4 tháng 4 2022

Ba đội công nhân cùng làm việc. Trong một giờ đội thứ nhất là được 2 9 công việc, đội thứ hai là được 1 3 công việc, đội thứ ba làm được 5 27 công việc. a) Theo em trong một giờ đội nào làm được khối lượng công việc nhiều nhất. Đội nào làm được khối lượng công việc ít nhất? Vì sao? b) Nếu làm chung thì mỗi giờ cả ba đội làm được bao nhiêu phần công...

Đọc tiếp

#Toán lớp 6

1

HN

Hiếu Nguyễn

4 tháng 4 2022

2 9 là 2 đến 9 hay 29 rồi mấy số còn lại cx y như 2 9

Đúng(1)

L

lynn

4 tháng 4 2022

là 2/9 đó

Đúng(1)

PT

Pham Trong Bach

4 tháng 1 2019

Hai đội công nhân cùng làm một công việc thì hoàn thành công việc đó trong 24 giờ. Nếu đội thứ nhất làm 10 giờ, đội thứ hai làm 15 giờ thì cả hai đội làm được một nửa công việc. Tính thời gian đội một làm một mình xong công việc.

#Toán lớp 8

1

CM

Cao Minh Tâm

4 tháng 1 2019

Gọi thời gian để đội một làm một mình hoàn thành công việc là x giờ (x > 24)

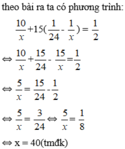
Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán năng suất | Toán lớp 8

Vậy thời gian để đội một làm mình hoàn thành công việc là 40 giờ

Đúng(1)

LH

Lê Hoài Duyên

16 tháng 2 2019 - olm

Hai đội công nhân cùng làm một công việc thì hoàn thành công việc đó trong 24 giờ. Nếu đội thứ nhất làm 10 giờ, đội thứ hai làm 15 giờ thì cả hai đội làm được một nửa công việc. Tính thời gian mỗi đội làm một mình để xong công việc.

#Toán lớp 8

1

PB

Pham Binh Minh

16 tháng 2 2019

Gọi a, b lần lượt là số phần công việc mà đội I và đội II làm được trong 1h
Vì 2 đội cùng làm việc thì hoàn thành công việc trong 24 giờ nên trong 1giờ cả 2 đội làm được 1 công việc :
<=> a + b = 1( 1 ) 24
24
Trong 10 giờ, đội I làm được 10.a phần công việc, trong 15 giờ đội II làm được 15.b phần công việc.
Vì khi đó cả 2 đội làm được 1 công việc nên :
10.a + 15.b = 1 ( 2 )
2
Từ ( 1 ) và ( 2 ) giải được a = 1 => Đội I làm trong 1 : 1 = 40 giờ thì xong công việc :
40 40
b = 1 => Đội II làm trong 1 : 1
60 60
= 60 giờ thì xong công việc.
Đáp số : 60 giờ

Chịu khó suy nghĩ là ra ngay thôi !!!

tk mk nha

Đúng(1)

TN

Trần Nhật Quỳnh

26 tháng 3 2017 - olm

Một đội công nhân cùng làm việc trong 3 ngày thì xong một công việc. Biết ngày đầu đội công nhân làm được 1/3 công việc. Lượng công việc làm được trong ngày thứ nhất bằng 2/3 ngày thứ hai. Vậy ngày thứ ba đội công nhân đó làm được …

#Toán lớp 4

5

D

DanAlex

26 tháng 3 2017

Ngày thứ hai đội đó làm được số phần công việc là:

(1/3)/(2/3)=1/2(công việc)

Cả hai ngày đội đó làm được số phần công việc là:

(1/2)+(1/3)=5/6(công việc)

Ngày thứ 3 đội đó làm được số phần công việc là:

1-(5/6)=1/6(công việc)

Vậy ngày thứ 3 người đó làm được 1/6 công việc

Đúng(0)

TN

Trần Nhật Quỳnh

26 tháng 3 2017

Nếu coi công việc đó gồm 6 phần bằng nhau thì ngày đầu làm được 2 phần như thế, ngày thứ hai làm được 3 phần như thế
Theo bài ra ta có sơ đồ:
Tổng số phần công việc là: ......................!----!----!----!----!----!----!
Số phần công việc làm được ngày đầu: ......!----!----!
Số phần công việc làm được ngày thứ hai: .!----!----!----!
Suy ra: Số phần công việc làm được ngày thứ ba là: 6 - 2 - 3 = 1 (phần)
Vậy: Ngày thứ ba đội công nhân đó làm được 1/6 công việc

Đúng(0)

D

dizacjungle

23 tháng 6 2023

Bài 2. (1,0 điểm) Ba đội công nhân cùng chuyển một khối lượng gạch như nhau. Thời gian để đội thứ nhất, đội thứ hai và đội thứ ba làm xong công việc lần lượt là 2 giờ, 3 giờ, 4 giờ. Tính số công nhân tham gia làm việc của mỗi đội, biết rằng số công nhân của đội thứ ba ít hơn số công nhân của đội thứ hai là 5 người và năng suất lao động của các công nhân là như nhaugiúp t với...

Đọc tiếp

#Toán lớp 7

2

T

Tuyet

23 tháng 6 2023

Gọi số công nhân 3(đội 1,2,3) đội lần lượt là $x,y,z$

Số công nhân của đội 3 ít hơn số công nhân của đội 2 là 5 người nên :

$y-z=5$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta đc:

$\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{4}}=\dfrac{y-z}{\dfrac{1}{3}-\dfrac{1}{4}}=60$

Suy ra x = 60.$\dfrac{1}{2}$ = 30 , y = 60.$\dfrac{1}{3}$ = 20, z = 60.$\dfrac{1}{4}$ =15

Vậy số công nhân tham gia làm việc của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là 30 người, 20 người, 15 người

Đúng(2)

NL

Nguyễn Lê Phước Thịnh

23 tháng 6 2023

Gọi số công nhân của đội 1;2;3 lần lượt là a,b,c

Theo đề, ta có: 2a=3b=4c và b-c=5

=>a/6=b/4=c/3 và b-c=5

Áp dụng tính chất của DTSBN, ta được:

a/6=b/4=c/3=(b-c)/(4-3)=5/1=5

=>a=30; b=20; c=15

Đúng(2)

QT

Quoc Tran Anh Le

Giáo viên

19 tháng 9 2023

Ba đội công nhân làm đường được giao ba khối lượng công việc như nhau. Đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai trong 5 ngày và đội thứ ba trong 6 ngày. Tính số công nhân của mỗi đội biết đội thứ nhất nhiều hơn đội thứ hai là 3 người và năng suất của các công nhân là như nhau trong suốt quá trình làm...

Đọc tiếp

#Toán lớp 7

1

HQ

Hà Quang Minh

Giáo viên

19 tháng 9 2023

Gọi số công nhân mỗi đội lần lượt là x,y,z (người) $(x,y,z \in N^*).$

Vì số công nhân của đội thứ nhất nhiều hơn số công nhân của đội thứ hai là 3 người nên $x – y = 3$.

Vì khối lượng công việc là như nhau và năng suất của các máy như nhau nên số công nhân và thời gian hoàn thành là 2 đại lượng tỉ lệ nghịch.

Áp dụng tính chất của hai đại lượng tỉ lệ nghịch, ta có:

$4x=5y=6z\Rightarrow \dfrac{x}{{\dfrac{1}{4}}} = \dfrac{y}{{\dfrac{1}{5}}} = \dfrac{z}{{\dfrac{1}{6}}}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\begin{array}{l} \Rightarrow \dfrac{x}{{\dfrac{1}{4}}} = \dfrac{y}{{\dfrac{1}{5}}} = \dfrac{z}{{\dfrac{1}{6}}} = \dfrac{{x - y}}{{\dfrac{1}{4} - \dfrac{1}{5}}} = \dfrac{3}{{\dfrac{1}{{20}}}} = 3:\dfrac{1}{{20}} = 3.20 = 60\\ \Rightarrow x = 60.\dfrac{1}{4} = 15\\y = 60.\dfrac{1}{5} = 12\\z = 60.\dfrac{1}{6} = 10\end{array}$

Vậy 3 đội có lần lượt là 15; 12 và 10 công nhân.

Đúng(1)

D

d.chi

18 tháng 2 2022

3. Một đội công nhân ngày thứ nhất làm được 2/9 phần công việc, ngày thứ hai làm được 4/9 phần công việc, ngày thứ ba làm dược 1/3 phần công việc. Hỏi cả ba ngày đội công nhân đó làm được bao nhiêu phần công việc ?

#Toán lớp 4

9

D

Dark_Hole

18 tháng 2 2022

Cả ba ngày đó đội công nhân làm đc sô phần công việc là

$\frac{2}{9}$ + $\frac{4}{9}$ + $\frac{1}{3}$ = $\frac{9}{9}$ = 1

vậy trong ba ngày đó đội công nhân là làm hết công việc nhé

Đúng(2)

HT

Huỳnh Thùy Dương

18 tháng 2 2022

Cả ba ngày đội công nhân làm công việc là :

2/9 + 4/9 + 1/3 = 1 ( công việc )

Đúng(2)

DQ

Đỗ Quang Vinh

7 tháng 12 2016 - olm

Ba đội công nhân làm xong công việc trong 13567 ngày, đội thứ nhất làm 1/3 số giờ mỗi ngày; đội thứ hai làm xong công việc gấp 5 lần đội thứ nhất; đội thứ ba là số giờ còn lại. Hỏi đội thứ ba còn phải làm bao nhiêu giờ?

#Toán lớp 5

0

N1

Nguyễn_kiều_lan 1234

19 tháng 8 2020 - olm

Có ba đội cùng hoàn thành một con đường .Một ngày, đội thứ nhất làm được 5/27 con đường , đội thứ 2 làm được 6/29 con đường , đội thứ 3 làm được 7/25 con đường . Theo em trong 1 ngày đội nào làm được lượng công việc nhiều nhất

#Toán lớp 6

0

SD

Son Dinh

20 tháng 1 2022

Hai đội công nhân cùng làm chung thì sau 4 giờ sẽ hoành thành công việc . Nếu đội thứ nhất làm trong 3 giờ rồi đội thứ hai làm tiếp trong 4 giờ mới được 0,8 công việc . Hỏi mội đội làm riêng thì bao lâu sẽ xong công việc

#Toán lớp 9

1

KV

Kiều Vũ Linh

20 tháng 1 2022

Gọi $x\left(giờ\right),y\left(giờ\right)$ lần lượt là thời gian của đội thứ nhất và đội thứ hai làm riêng xong công việc (x, y > 0)

Trong một giờ hai đội làm được: $\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}$ (công việc)

Đội thứ nhất làm trong 3 giờ rồi đội thứ hai làm tiếp trong 4 giờ được 0,8 công việc nên ta có:

$\dfrac{3}{x}+\dfrac{4}{y}=0,8$

Ta có hệ phương trình:

$\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\\dfrac{3}{x}+\dfrac{4}{y}=0,8\end{matrix}\right.$

Đặt $u=\dfrac{1}{x};v=\dfrac{1}{y}$, ta có:

$\left\{{}\begin{matrix}u+v=\dfrac{1}{4}\\3u+4v=0,8\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}4u+4v=1\\3u+4v=0,8\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}4u+4v=1\\u=\dfrac{1}{5}\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}4.\dfrac{1}{5}+4v=1\\u=\dfrac{1}{5}\end{matrix}\right.$

$\Leftrightarrow\left\{{}\begin{matrix}v=\dfrac{1}{20}\\u=\dfrac{1}{5}\end{matrix}\right.$

*) $u=\dfrac{1}{5}\Leftrightarrow\dfrac{1}{x}=\dfrac{1}{5}\Leftrightarrow x=5$ (nhận)

*) $v=\dfrac{1}{20}\Leftrightarrow\dfrac{1}{y}=\dfrac{1}{20}\Rightarrow y=20$ (nhận)

Vậy đội thứ nhất làm riêng trong 5 giờ xong công việc

đội thứ hai làm riêng trong 20 giờ xong công việc

Đúng(2)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP