Mọi người giải hộ em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



4:
a: góc CEH+góc CDH=180 độ
=>CDHE nội tiếp
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
góc EHA=góc DHB
=>ΔHEA đồng dạng với ΔHDB
=>HE/HD=HA/HB
=>HE*HB=HD*HA


Câu 3:
a)
CTPT xủa X là CnH2n+2O
\(n_{CO_2}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\Rightarrow n_{C_nH_{2n+2}O}=\dfrac{0,4}{n}\left(mol\right)\)
=> \(n_{H_2O}=\dfrac{\dfrac{0,4}{n}.\left(2n+2\right)}{2}=\dfrac{0,4}{n}\left(n+1\right)\left(mol\right)\)
Mà \(n_{H_2O}=\dfrac{9}{18}=0,5\left(mol\right)\)
=> n = 4
=> CTPT: C4H10O
b) \(n_{C_4H_{10}O}=\dfrac{0,4}{4}=0,1\left(mol\right)\)
=> m = 0,1.74 = 7,4 (g)
c)
(1) \(CH_3-CH_2-CH_2-CH_2OH\)
(2) \(CH_3-CH_2-CH\left(OH\right)-CH_3\)
(3) \(CH_3-C\left(CH_3\right)\left(OH\right)-CH_3\)
(4) \(CH_3-CH\left(CH_3\right)-CH_2OH\)
(5) \(CH_3-CH_2-CH_2-O-CH_3\)
(6) \(CH_3-CH\left(CH_3\right)-O-CH_3\)
(7) \(CH_3-CH_2-O-CH_2-CH_3\)
d)
X là \(CH_3-C\left(CH_3\right)\left(OH\right)-CH_3\) (2-metylpropan-2-ol)

\(b,\Leftrightarrow\left\{{}\begin{matrix}m+2=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=-1\\ c,\text{PT giao Ox: }y=0\Leftrightarrow\left(m+2\right)x-m=0\\ \text{Thay }x=2\Leftrightarrow2m+4-m=0\\ \Leftrightarrow m=-4\\ d,\text{PT giao Ox và Oy: }\\ y=0\Leftrightarrow x=\dfrac{m}{m+2}\Leftrightarrow A\left(\dfrac{m}{m+2};0\right)\Leftrightarrow OA=\left|\dfrac{m}{m+2}\right|\\ x=0\Leftrightarrow y=-m\Leftrightarrow B\left(0;-m\right)\Leftrightarrow OB=\left|m\right|\\ \Delta OAB\text{ cân }\Leftrightarrow OA=OB\Leftrightarrow\left|\dfrac{m}{m+2}\right|=\left|m\right|\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{m}{m+2}=m\\\dfrac{m}{m+2}=-m\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\left(m+1\right)=0\\m\left(m+3\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-1\\m=-3\end{matrix}\right.\)

a: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng với ΔBHA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: BA^2=BH*BC
=>BM^2=BH*BC
=>BM/BH=BC/BM
=>ΔBMC đồng dạng với ΔBHM
=>góc BMH=góc BCM

a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp

 mọi người giải hộ em với ạ,em cảm ơn
mọi người giải hộ em với ạ,em cảm ơn
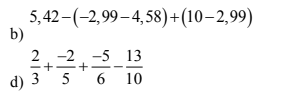



 mọi người giải hộ em ạ , em cảm ơn nhiều . Phần kia G
mọi người giải hộ em ạ , em cảm ơn nhiều . Phần kia G
`Answer:`
`x^2+4x+7=(x+4)\sqrt{x^2+7}`
Ta đặt `v=\sqrt{x^2+7}` và `v>=\sqrt{7}`
`=>v^2=x^2+7`
Phương trình trở thành: `v^2+4x=(x+4)v`
`<=>v^2-xv+4x-4v=0`
`<=>(v-4)(v-x)=0`
`<=>v=4` hoặc `v=x`
Với `v=4` ta được: `\sqrt{x^2+7}=4`
`=>x^2+7=16`
`<=>x^2=9`
`<=>x=+-3`
Với `v=x` ta được: `\sqrt{x^2+7}=x`
\(\Leftrightarrow\hept{\begin{cases}x\ge0\\x^2+7=x^2\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge0\\7=0\text{(Vô lý)}\end{cases}}\Leftrightarrow x\in\varnothing\)
Đặt \(\sqrt{x^2+7}=t>0\)
Pt trở thành:
\(t^2-\left(x+4\right)t+4x=0\)
\(\Leftrightarrow t^2-xt-4t+4x=0\)
\(\Leftrightarrow t\left(t-x\right)-4\left(t-x\right)=0\)
\(\Leftrightarrow\left(t-x\right)\left(t-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=4\\t=x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+7}=4\\\sqrt{x^2+7}=x\left(x\ge0\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+7=16\\x^2+7=x^2\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow x=\pm3\)