Cho hai điểm A, B nằm trên đường trung trực của đoạn thẳng BC sao cho A, B thuộc hai nửa mặt phẳng bờ BC. Chứng minh AB CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 11 2021
a) Ta có: ^BAH = ^BCA (vì 2 góc này cùng phụ với ^B)
Mà: ^MAC = ^BCA (tg MAC cân tại M vì Tg ABC vuông tại A có AM là trung tuyến)
Nên: ^BAH = ^MAC (4)
b) Tg AMD cân tại M (vì MA=MD) => ^D = ^DAM (1)
Ta có: MD//AH ( vì MD_I_ HM, AH _I_ HM )
Nên: ^D = ^DAH (2)
(1)(2) => ^DAM = ^DAH (3) => AD là p/g của ^HAM (5)
(3)(4) => ^BAH + ^DAH = ^MAC + ^DAM <=> ^BAD=^CAD => AD là p/g của ^BAC (6)
(5)(6) => AD là p/g chung của ^HAM và ^BAC
c) Ta có: AEDF là hcn ( vì ^E=^F=^A=90o )
Mà: AD là p/g của ^EAC (cmt)
Nên: AEDF là hình vuông
d) Tg DBE (^DEA=90o) và tg DCF (^DFC=90o) có:
DE = DF (AEDF là hình vuông)
DB = DC (MD là đường trung trực của BC)
Nên: Tg DBE = tg DCF (ch-cgv)
CM
20 tháng 3 2019
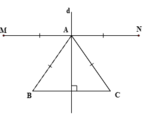
Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN
CM
5 tháng 7 2019
a) B A H ^ + M A C ^ vì cùng phụ với A B C ^
b) A 1 ^ = C 1 ^ (1) (chứng minh a)
Mà DABC vuông có AM là trung tuyến nên DAMC cân tại M C 1 ^ = A 4 ^ (2).
Từ (1) và (2) suy ra A 1 ^ = A 4 ^ (3)
D thuộc đường trung trực của BC.
Þ DM ^ BC = {M}
Þ D 1 ^ = A 2 ^
Vì DM = MA (giả thiết) ⇒ M 1 ^ = A 3 ^ ⇒ A 2 ^ = A 3 ^ (4)
Từ (3) và (4) Þ AD là phân giác chung của M A H ^ & C A B ^
c) Theo cách vẽ và kết quả câu b), ta có AEDF là hình vuông.
d) DDBE = DDCF (cạnh huyền - cạnh góc vuông)
15 tháng 5 2022
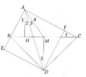
a: Vì A nằm trên đường trung trực của BC
nên AB=AC
Vì D nằm trên đường trung trực của BC
nen DB=DC
Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó:ΔABD=ΔACD
b: Gọi giao điểm của BC và AD là O
=>O là trung điểm của BC
Trường hợp 1: A,D nằm cùng phía
\(AO=\sqrt{AB^2-BO^2}=4.5\left(cm\right)\)
\(DO=\sqrt{6.5^2-6^2}=2.5\left(cm\right)\)
=>AD=2(cm)
TH2: A,D khác phía
\(AO=\sqrt{7.5^2-6^2}=4.5\left(cm\right)\)
\(DO=\sqrt{6.5^2-6^2}=2.5\left(cm\right)\)
AD=AO+DO=7(cm)
CM
15 tháng 8 2017
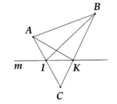
a) Vì hai điểm A, B nằm trên hai nửa mặt phẳng đối nhau bờ m nên đoạn thẳng AB cắt đường thẳng m.
b) Từ câu a), ta suy ra điểm K nằm giữa hai điểm B, C nên tia AK nằm giữa hai tia AB và AC.
Tương tự, ta có điểm I nằm giữa hai điểm A, C nên tia BI nằm giữa, hai tia BA, BC.
c*) Từ câu b), ta suy ra tia BI nằm giữa hai tia BA,BK nên tia BI cắt đoạn thẳng AK tại một điểm nằm giữa A và K.
Lập luận tương tự, ta có tia AK cắt đoạn thẳng BI tại một điểm nằm giữa B và I. Từ đó suy ra hai đoạn thẳng AK và BI cắt nhau.