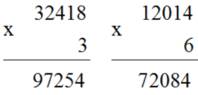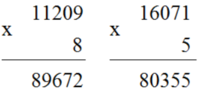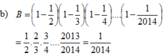Tính: (12014 + 22014 + 32014 + 42014 + 52014) : 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
S
29 tháng 12 2020
S = 1 + 3 + 32 + 33 +... + 32014
3S = 3 + 32 + 33 + 34 + ... + 32015
3S - S = ( 3 + 32 + 33 + 34 + ... + 32015) - (1 + 3 + 32 + 33 +... + 32014)
2S = 32015 - 1
S = \(\dfrac{3^{2015}-1}{2}\)
PT
1
3 tháng 2 2021
Ta có:
A= 52014-52013+52012⋮105
A= 5^2011(5^3- 5^2)+5
A=5^2011(125- 25)+5
A= 5^2011. 105
=> A:105(đpcm)
3 tháng 2 2021
5^2014-5^2013+5^2012
=5^2012(5^2-5^1+1)
=5^2012.21 =5^2011.5.21
=5^2011.105
Vậy 5^2014-5^2013+5^2012 chia hết cho 105
chúc bạn học tốt
NG
1
26 tháng 8 2021
\(S=1-2+2^2-2^3+...+2^{2012}-2^{2013}\)
\(\Rightarrow2S=2-2^2+2^3-2^4+...+2^{2013}-2^{2014}\)
\(\Rightarrow2S+S=2-2^2+2^3-...-2^{2014}+1-2^2-2^3+...-2^{2013}\)
\(\Rightarrow3S=1-2^{2014}\)\(\Rightarrow3S-2^{2014}=1-2^{2015}\)
DT
0
CM
24 tháng 8 2018
Ta có 2 + 1 2017 = C 2017 0 .2 2017 + C 2017 1 .2 2016 + ... + C 2017 2017 .2 0
2 − 1 2017 = C 2017 0 .2 2017 + C 2017 1 .2 2016 . − 1 + ... + C 2017 2017 .2 0 . − 1 2017
Trừ từng vế hai đẳng thức trên ta được:
3 2017 − 1 = 2 C 2017 1 .2 2016 + C 2017 3 .2 2014 + ... + C 2017 2017 .2 0
Vậy M = 3 2017 − 1 2
Chọn đáp án D.
6 tháng 4 2020
Bài 1:
Ta có: \(3n+1⋮n-1\)
\(\Leftrightarrow3n-3+4⋮n-1\)
mà \(3n-3⋮n-1\)
nên \(4⋮n-1\)
\(\Leftrightarrow n-1\inƯ\left(4\right)\)
\(\Leftrightarrow n-1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{2;0;3;-1;5;-3\right\}\)(tm)
Vậy: \(n\in\left\{2;0;3;-1;5;-3\right\}\)