Mn ơi mn giúp mk bài này vs ạ (mình đang cần gấp🥺🥺🥺). Thanks mn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

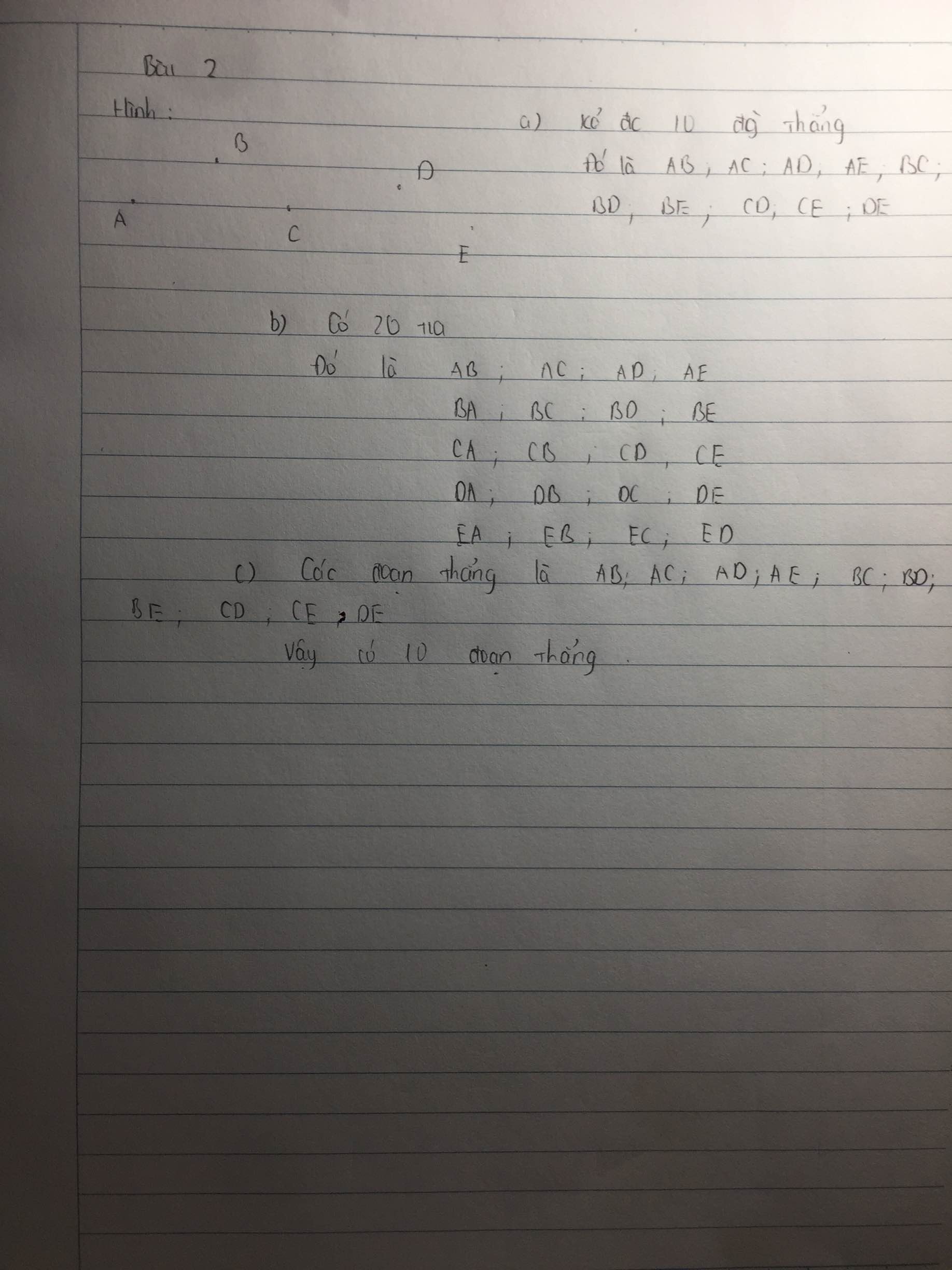



Dấu hiệu là số lượng hsinh nữ trong 1 trường THCS
Có 30GT
| GT(x) | 6 | 12 | 14 | 16 | 18 | 17 | 19 | 20 | 13 | 10 15 25 |
| Tần số (n) | 1 | 2 | 3 | 5 | 3 | 4 | 3 | 3 | 1 | 1 3 1. N= 30 |
Có 12 GT khác nhau
Giá trị có tần số lớn(nhỏ) nhất là 16(6;13;10;25)
Mốt của dấu hiệu 14 --> 17
a) dấu hiệu cần tìm là : số lượng học sinh nữ của mỗi lớp
- Dấu hiệu đó có tất cả 30 giá trị
b) bảng tần số giờ ko lập dc ở đây

\(x^4-8x=x\left(x^3-8\right)=x\left(x-2\right)\left(x^2+2x+4\right)\)
\(x^2-y^2-6x+9=\left(x^2-6x+9\right)-y^2=\left(x-3\right)^2-y^2=\left(x+y-3\right)\left(x-y-3\right)\)

a: 2+5/6=12/6+5/6=17/6
b: 5/12+3/4+1/3=5/12+9/12+4/12=18/12=3/2
c: 2/3+3/4=8/12+9/12=17/12

a) Vì ABCD là hình bình hành ( gt )
⇒ AD // BC
F ∈ BC
⇒ AD // BF
⇒ ∠EDA = ∠EFB ( hai góc so le trong )
Xét △AED và △BEF, có :
∠EDA = ∠EFB ( cmt )
∠AED = ∠FEB ( hai góc đối đỉnh )
⇒ △AED ∼ △BEF (g-g)
b) Vì ABCD là hình bình hành ( gt )
⇒ AB // CD
E ∈ AB
⇒ BE // CD
Xét △FDC, có :
BE // CD ( cmt )
E ∈ DF ; B ∈ DC
⇒ \(\dfrac{FB}{FC}=\dfrac{EB}{DC}\) (Hệ quả của định lí Ta-let)
⇒ \(\dfrac{BF}{BE}=\dfrac{FC}{DC}\) (1)
Vì △AED ∼ △BEF ( cmt )
⇒ \(\dfrac{AE}{BE}=\dfrac{AD}{BF}\) (TSDD)
⇒ \(\dfrac{AE}{AD}=\dfrac{BE}{BF}\) (2)
Từ (1) và (2) ⇒ \(\dfrac{AE}{AD}=\dfrac{CF}{CD}\)
⇒ AD.CD = AE.CF
c) Xét △DGC, có :
AE // DC ( cmt )
G ∈ AC ; G ∈ DE
⇒ \(\dfrac{DG}{DE}=\dfrac{GC}{AC}\) (Hệ quả của định lí Ta-let) (3)
Xét △FGC, có :
AD // CF ( cmt )
G ∈ AC ; G ∈ DF
⇒ \(\dfrac{DG}{DF}=\dfrac{AG}{AC}\) (Hệ quả của định lí Ta-let) (4)
Từ (3) và (4) ⇒ \(\dfrac{DG}{DE}+\dfrac{DG}{DF}=\dfrac{GC}{AC}+\dfrac{AG}{AC}\)
⇒ \(\dfrac{DG}{DE}+\dfrac{DG}{DF}\) = 1
⇒ \(\dfrac{1}{DG}\left(\dfrac{DG}{DE}+\dfrac{DG}{DF}\right)=\dfrac{1}{DG}\)
⇒ \(\dfrac{1}{DG}=\dfrac{1}{DE}+\dfrac{1}{DF}\)


 Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều
Mn giải giúp mik vs ạ 🥺 mình đang cần gấp. Cảm ơn mn nhiều