Giúp mình với .Mình xin cảm ơn trước
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
9 tháng 11 2021
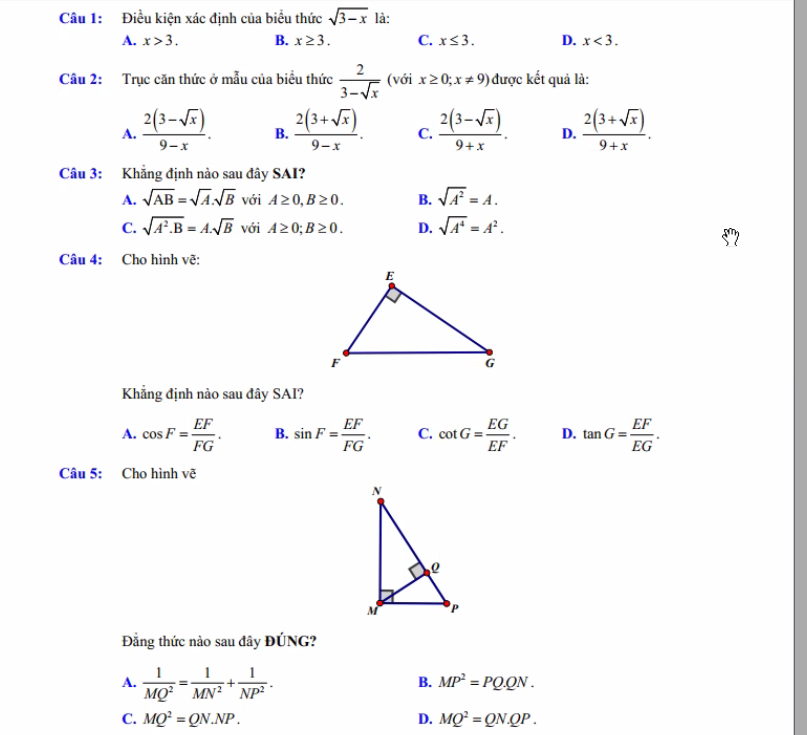
Câu 1: ĐKXĐ: $3-x\geq 0\Leftrightarrow x\leq 3$
Đáp án C
Câu 2:
\(\frac{2}{3-\sqrt{x}}=\frac{2(3+\sqrt{x})}{(3-\sqrt{x})(3+\sqrt{x})}=\frac{2(3+\sqrt{x})}{9-x}\)
Đáp án B.
AH
Akai Haruma
Giáo viên
9 tháng 11 2021
Câu 3: B
Vì $\sqrt{A^2}=|A|$ chứ không phải $A$
Câu 4: B
Câu 5: D
TP
13 tháng 7 2021
A: Fe
B: Fe2(SO4)3
C : Fe(OH)3
D: Fe2O3
X: H2SO4 đặc nóng
Y: NaOH
Z : CO
PTHH:
2Fe + 6H2SO4 → Fe2(SO4)3 + 3SO2 + 6H2O
Fe2(SO4)3 + 6NaOH → 2Fe(OH)3 + 3Na2SO4
2Fe(OH)3 ------to-------> Fe2O3 + 3H2O
Fe2O3 + 3CO --------> 2Fe + 3CO2
2H
giúp mình với ạ,mình xin cảm ơn trước
1
21 tháng 11 2021
Gọi x,y,z là số học sinh khối 6, 7, 8
(x,y,z>0, đvị là học sinh)
Đã biết khối học sinh lớp 8 ít hơn số hs khối 6 là 120 hs
x-z=120
x, y, z tỉ lệ với 8, 7, 5
x/8=y/7=z/5
Áp dụng tính chất dãy tỉ số bằng nhau có:
x/8=y/7=z/5= x-z/8-5=120/3=40
=> x/8= 40 => x=40.8=320 => số hs khối 6 là 320 hs
y/7= 40 y=40.7= 280 số hs khối 7 là 280 hs
z/5= 40 z=40.5=200 số hs khối 8 là 200 hs
HT
1
TM
10 tháng 8 2021
PTHH: Al2O3+6HCl➝2AlCl3+3H2O(1)
a)nAl2O3=\(\dfrac{10,2}{102}\)=0,1(mol)
mHCl=\(\dfrac{5\%.219}{100\%}\)=10,95(g)
⇒nHCl=\(\dfrac{10,95}{36,5}\)=0,3(mol)
Xét tỉ lệ Al2O3:\(\dfrac{0,1}{1}\)=0,1
Xét tỉ lệ HCl:\(\dfrac{0,3}{6}\)=0,05
⇒HCl pứng hết,Al2O3 còn dư
Theo PTHH(1) ta có nAl2O3 pứng=\(\dfrac{nHCl}{6}\)=\(\dfrac{0,3}{6}\)=0,05(mol)
⇒nAl2O3 dư=nAl2O3ban đầu-nAl2O3 pứng=0,1-0,05=0,05(mol)
⇒mAl2O3 dư=0,05.102=5,1(g)
b) C%HCl=\(\dfrac{0,3.36,5}{219+10,2}\).100%=4,8%
nAlCl3=0,1(mol)
⇒C%AlCl3=\(\dfrac{0,1.136,5}{10,2+219}\).100%=6%
H
2
NL
1
21 tháng 10 2021
\(d,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=2+\sqrt{x+1}\\ \Leftrightarrow x-1=2+x+1+4\sqrt{x+1}\\ \Leftrightarrow4\sqrt{x+1}=-4\Leftrightarrow x\in\varnothing\left(4\sqrt{x+1}\ge0\right)\\ g,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow x+\sqrt{2x-1}+x-\sqrt{2x-1}+2\sqrt{\left(x+\sqrt{2x-1}\right)\left(x-\sqrt{2x-1}\right)}=2\\ \Leftrightarrow2x+2\sqrt{x^2-2x+1}=2\\ \Leftrightarrow\sqrt{\left(x-1\right)^2}=\dfrac{2-2x}{2}=1-x\\ \Leftrightarrow\left|x-1\right|=1-x\\ \Leftrightarrow\left[{}\begin{matrix}x-1=1-x\left(x\ge1\right)\\x-1=x-1\left(x< 1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x\in R\end{matrix}\right.\)
NT
0
KN
2
cậu có học phú la ko