Ai giỏi toán làm hộ mình với
Cho tam giác nhọn ( AB<AC) có các đường cao BH và CK cắt nhau tại F
a) Chứng minh tam giác ABC ᔕ tam giác ACK
b) Chứng minh \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c) So sánh góc AKH và góc ACB
d) Chứng minh BE.BH+CE.CK=BC\(^2\)


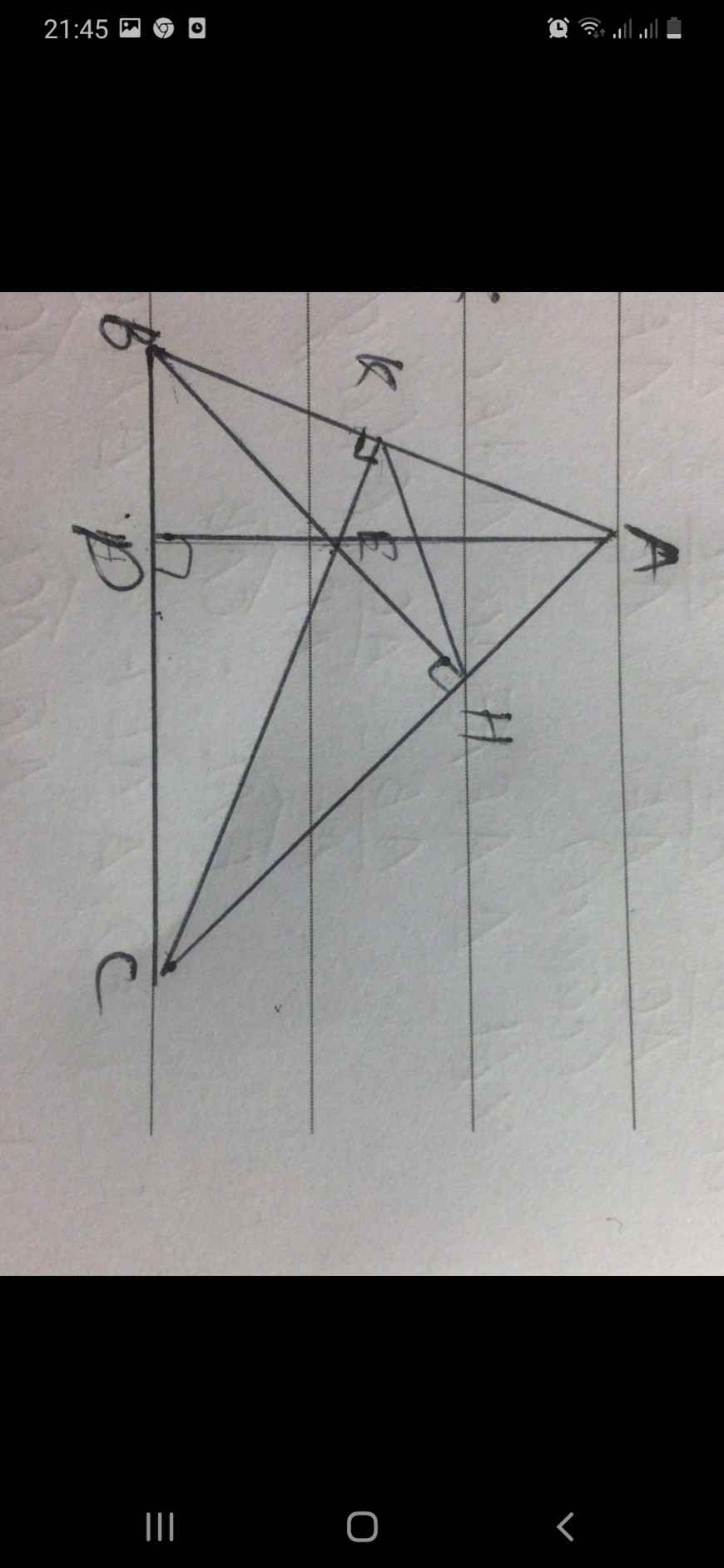

a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACK
b: Xét ΔKEB vuông tại K và ΔHEC vuông tại H có
\(\widehat{KEB}=\widehat{HEC}\)
DO đó: ΔKEB\(\sim\)ΔHEC
Suy ra: EK/EH=EB/EC
hay \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c: Xét ΔAKH và ΔACB có
AK/AC=AH/AB
góc A chung
Do đó: ΔAKH\(\sim\)ΔACB
Suy ra: \(\widehat{AKH}=\widehat{ACB}\)
Em cảm ơn ạ