so sánh: cs lời giải chi...
Đọc tiếp
so sánh: cs lời giải chi tiết
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MT
1
MT
1
TC
8 tháng 4 2022
\(N=\dfrac{\dfrac{2.2}{3}\left(\dfrac{1}{5}-\dfrac{1}{7}-\dfrac{1}{11}\right)}{\dfrac{6.6}{2}\left(\dfrac{1}{5}-\dfrac{1}{7}-\dfrac{1}{11}\right)}=\dfrac{4}{\dfrac{3}{\dfrac{36}{2}}}=24\)
MT
3
8 tháng 4 2022
\(=\dfrac{1}{2}\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+\dfrac{2}{9\cdot11}+\dfrac{2}{11\cdot13}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{10}{39}=\dfrac{5}{39}\)
NN
4
ND
2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
14 tháng 8 2023
\(\dfrac{7^{45}}{7}=7^{44}\)
\(49.7^{20}=7^2.7^{20}=7^{22}\)
\(\Rightarrow\dfrac{7^{45}}{7}=7^{44}>7^{22}=49.7^{20}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 8 2023
745 : 7 23 = 722
49 \(\times\) 720 = 72 \(\times\) 720 = 722
745 : 723 = 49 \(\times\) 720
NN
2
1 tháng 11 2020
\(31^{12}=\left(31^3\right)^4=29791^4\left(1\right)\)
\(27^{20}=\left(27^5\right)^4=14348907^4\left(2\right)\)
từ (1) và (2) => 31^12 <27^20
GQ
1 tháng 11 2020
31\(^{12}\)<32\(^{12}\)=(2\(^5\))\(^{12}\)=2\(^{60}\) (1)
27\(^{12}\)=(3\(^3\))\(^{20}\)=3\(^{60}\) (2)
=> 27\(^{20}\)>31\(^{12}\)
DT
5
2 tháng 11 2017
Có 2^285 = (2^3)^95 = 8^95
3^190 = (3^2)^95 = 9^95
Vì 8^95 < 9^95 nên 2^285 < 3^190
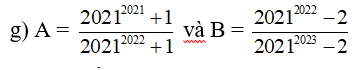
k) \(\dfrac{-209}{115}\) và \(\dfrac{-241}{131}\)
Ta có : \(\left(-209\right)\cdot131=-27379\)
\(\left(-241\right)\cdot115=-27715\)
Mà \(\left(-27715\right)< \left(-27379\right)\)
\(\Rightarrow\) \(\dfrac{-209}{115}>\dfrac{-241}{131}\)