cho hình chữ nhật ABCD có AB>AD.kẻ AH vuông góc với BD tại H.GọiM,N lần lượt là giao điểm đường thẳng AH với các đường thẳng CD,CB.
a) tính BD,AH khi AD=6cm,AB=8cm
b) chứng minh tam giác ABD đồng dạng với tam giác HBA và suy ra AB2=BH.BD
c)chứng minh \(\dfrac{1}{AH}\)=\(\dfrac{1}{AM}\)+\(\dfrac{1}{AN}\)


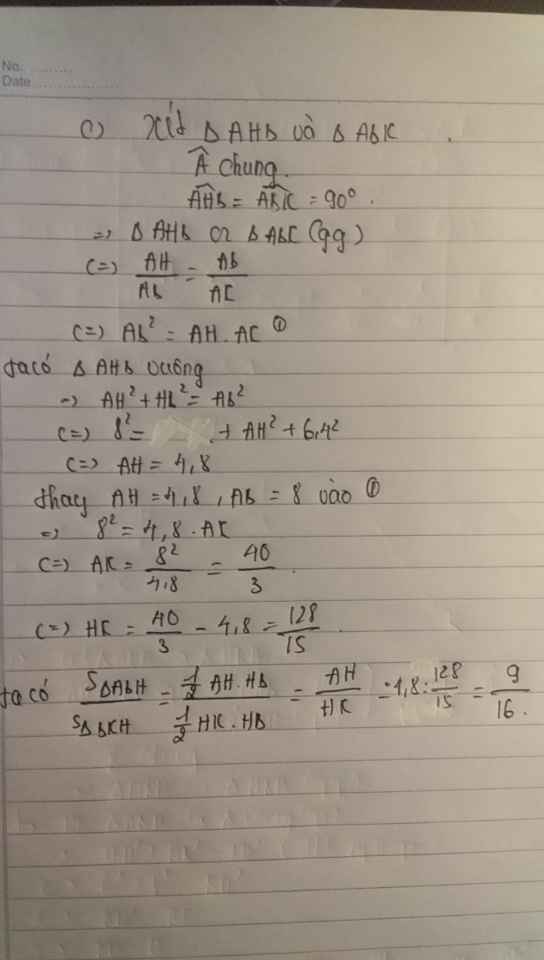
a: BD=căn 6^2+8^2=10cm
AH=6*8/10=4,8cm
b: Xét ΔABD vuông tại A và ΔHBA vuông tại H có
góc ABD chung
=>ΔABD đồng dạng với ΔHBA
=>BA/BH=BD/BA
=>BA^2=BH*BD