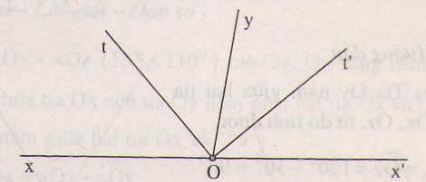
Cho 2 góc đối đỉnh \(\widehat{xOy}\) và \(\widehat{x'Oy'}\) gọi Ot là tia phân giác của góc \(\widehat{xOy}\),Ot' là tia đối của tia Ot, chứng minh Ot' là tia phân giác của \(\widehat{x'Oy'}\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 8 2023
Ot là phân giác của góc xOy
=>góc xOt=góc yOt=góc xOy/2
Ot' là phân giác của góc x'Oy'
=>góc x'Ot'=góc y'Ot'=góc x'Oy'/2
mà góc x'Oy'=góc xOy
nên góc xOt=góc yOt=góc x'Ot'=góc yOt'
=>góc x'Ot'=góc xOt
=>góc xOt+góc xOt'=180 độ
=>Ot và Ot' là hai tia đối nhau
BD
21 tháng 6 2017
ta có xOy và x'Oy là 2 góc đối đỉnh
suy ra xOy=x'Oy
mà Ot là tia phân giác của xOy
Ot' là tia phân giác cuat x'Oy'
nên Ot và Ot' là 2 tia đối nhau .
KN
10 tháng 6 2019
+) Tính \(\widehat{yOx'}\)
Ta có: \(\widehat{yOx'}+\widehat{xOy}=180^0\)(kề bù)
hay \(\widehat{yOx'}+36^0=180^0\)
\(\Leftrightarrow\widehat{yOx'}=180^0-36^0\)
\(\Leftrightarrow\widehat{yOx'}=144^0\)
Vậy \(\widehat{yOx'}=144^0\)
+) Tính \(\widehat{y'Ox'}\)
Vì hai đường thẳng xx' và yy' cắt nhau tại O nên \(\widehat{y'Ox'}\) và \(\widehat{yOx}\)là hai góc đối đỉnh.
\(\Rightarrow\widehat{y'Ox'}=\widehat{xOy}=36^0\)
Vậy \(\widehat{y'Ox'}=36^0\)
+) Tính \(\widehat{y'Ox}\)
Vì hai đường thẳng xx' và yy' cắt nhau tại O nên \(\widehat{y'Ox}\) và \(\widehat{yOx'}\)là hai góc đối đỉnh.
\(\Rightarrow\widehat{yOx'}=\widehat{xOy}'=144^0\)
Vậy \(\widehat{y'Ox}=144^0\)
b) Vì \(\widehat{y'Ox'}=\widehat{xOy}\)mà Ot là tia phân giác của \(\widehat{xOy}\),mà Ot' là tia phân giác của \(\widehat{x'Oy'}\)nên Ot và Ot' (điều hiển nhiên)
18 tháng 4 2017
Giải:
Hai góc xOy và x'Oy là hai góc kề bù mà = 1000 nên
= 1800 - 1000 = 800.
Giải tương tự bài 33, ta được ,