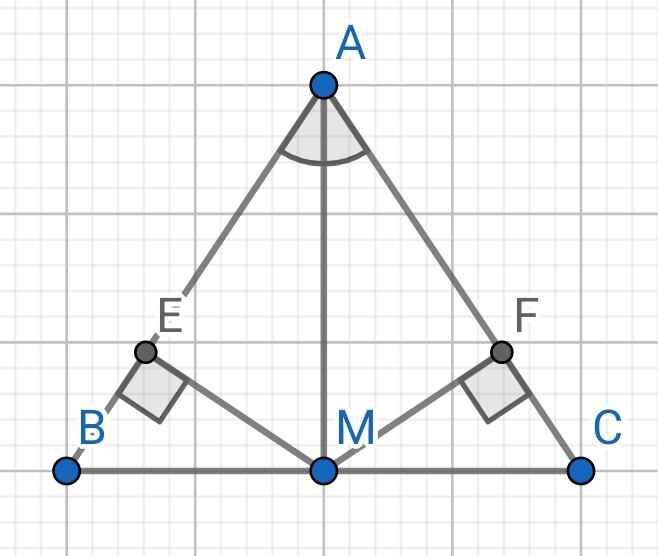
Cho tam giác ABC có góc A= 40o, AB=AC, AM là đường tuyến của tâm giác ABC a/ Chứng minh ΔAMB=ΔAMCb/ Chưng minh AM là tia phân giác của góc BAC và AM vuông góc BCc/ tính các góc của ΔAMB và ΔAMCd/ Gọi...

TQ

Trương Quang Trực lớp 7/8

31 tháng 3 2022

Cho tam giác ABC có góc A= 40o, AB=AC, AM là đường tuyến của tâm giác ABC a/ Chứng minh ΔAMB=ΔAMCb/ Chưng minh AM là tia phân giác của góc BAC và AM vuông góc BCc/ tính các góc của ΔAMB và ΔAMCd/ Gọi E,F lần lượt là trung điểm của AB và AC. C/m ME= MF và ΔEMF...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

8 tháng 7 2023

a: Xét ΔAMB và ΔAMC có
AM chung

MB=MC

AB=AC

=>ΔAMB=ΔAMC

b: ΔAMB=ΔAMC

=>góc MAB=góc MAC

=>AM là phân giác của góc BAC

ΔABC cân tại A có AM là trung tuyến

nên AM vuông góc BC

c: góc BAM=góc CAM=40/2=20 độ

góc B=góc C=90-20=70 độ

d: Xét ΔAEM và ΔAFM có

AE=AF

góc EAM=góc FAM

AM chung

=>ΔAEM=ΔAFM

=>ME=MF

=>ΔMEF cân tại M

Đúng(0)

T

tri3110(O_O)

24 tháng 12 2021

Cho tam giác ABC có AB = AC,M là trung điểm của BC.
a)Chứng minh: ΔAMB= ΔAMC
b)Chứng minh: AM là phân giác của góc BAC và AM là đường trung trực của BC.

cíu mik vứi

#Toán lớp 7

1

2A

2@2@

24 tháng 12 2021

tick mik nha bạn

a, +Xét tam giác ABM và ACM có:
AB=AC(Giả thiết) --
  AM là cạnh chung) I =>tam giác ABM=ACM (C-C-C)
  MB=MC(Giả thiết) --
b, +Ta có: tam giác ABM=ACM
=> góc AMB=góc AMC (2 góc tương ứng)
+Ta có:
góc AMB+AMC=180 ( 2 góc kề bù)
   AMB+AMB=180
   AMB = 90(độ)
=>AM vuông góc với BC
c, +Ta có: tam giác ABM=ACM
   => góc BAM=góc CAM(2 góc tương ứng)
   =>AM là tia phân giác của góc BAC
   hay AM là tia phân giác của góc A
Vậy a,tam giác ABM=ACM
   b,AM vuông góc với BC
   c,AM là tia phân giác của góc A

Đúng(0)

BT

bé thỏ cute

9 tháng 12 2021

cho ΔABC có AB=AC. Gọi M là trung điểm của BC. Chứng minh rằng:

a) ΔAMB=ΔAMC

b) AM là tia phân giác của góc BAC

c) AM vuông góc BC

d) Vẽ At là tia phân gác của góc ngoài ở đỉnh A của ΔABC. Chứng minh: At//BC

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

9 tháng 12 2021

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

Đúng(0)

DM

Đậu Minh Phú

5 tháng 4 2022

Cho tam giác ABC có AB = AC = 5cm, BC = 6cm. Đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC.a) Chứng minh ΔAMB = ΔAMC và AM là tia phân giác của góc A.b) Chứng minh AMc) Tính độ dài các đoạn thẳng BM và AM.d) Từ M vẽ ME AB (E thuộc AB) và MF AC (F thuộc AC). Tam giác MEF là tam giác gì? Vì sao? HELP...

Đọc tiếp

#Toán lớp 7

1

DM

Đinh Minh Đức

5 tháng 4 2022

a. Xét tam giác AMB và tam giác AMC:

AB = AC

AM chung

BM = CM (trung tuyến AM hạ từ A đến BC)

=> tam giác AMB = tam giác AMC

=> góc BAM = góc CAM (2 góc tương ứng)=>AM là tia phân giác của góc BACb. đề bài bị thiếuc. ta có BM = CM(cma) => BM = CM = $\dfrac{BC}{2}$= $\dfrac{6}{2}$= 3(cm) Áp dụng định lí Pi-ta-go vào tam giác ABM: AB² = BM² + AM²=> AM²= AB² - BM² AM² = 5² - 3² = 25 - 9 = 16(cm)=> AM = 4 cm

Đúng(2)

Y

ỵyjfdfj

24 tháng 12 2021

Bài 1: Cho tam giác ABC có AB = AC . Gọi M là trung điểm của BC . Chứng minh rằng:a) ΔAMB = ΔAMC .b) AM là tia phân giác của BAC .c) AM $\perp$ BC .d)Vẽ At là tia phân giác của góc ngoài ở đỉnh A của ΔABC. Chứng minh:At/ /BC...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

24 tháng 12 2021

a: Xét ΔAMB và ΔAMC có

AB=AC

AM chung

MB=MC

Do đó: ΔAMB=ΔAMC

Đúng(1)

KP

Khánh phạm

24 tháng 12 2023

Cho tam giác ABC có AB=AC, AM là phân giác của góc BAC ( M thuộc BC ):a, Chứng minh tam giác ABM= tam giác ACMb, Chứng minh M là trung điểm của BC và AM vuông góc BCc, Kẻ ME vuông góc AB ( E thuộc AB ) và MF vuông góc AC ( F thuộc AC ). Chứng minh...

Đọc tiếp

#Toán lớp 7

2

KV

Kiều Vũ Linh

24 tháng 12 2023

loading... a) Do AM là tia phân giác của ∠BAC (gt)

⇒ ∠BAM = ∠CAM

Xét ∆ABM và ∆ACM có:

AB = AC (gt)

∠BAM = ∠CAM (cmt)

AM là cạnh chung

⇒ ∆ABM = ∆ACM (c-g-c)

b) Do ∆ABM = ∆ACM (cmt)

⇒ BM = CM (hai cạnh tương ứng)

⇒ M là trung điểm của BC

Do ∆ABM = ∆ACM (cmt)

⇒ ∠AMB = ∠AMC (hai góc tương ứng)

Mà ∠AMB + ∠AMC = 180⁰ (kề bù)

⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰

⇒ AM ⊥ BC

c) Do ∠BAM = ∠CAM (cmt)

⇒ ∠EAM = ∠FAM

Xét hai tam giác vuông: ∆AME và ∆AMF có:

AM là cạnh chung

∠EAM = ∠FAM (cmt)

⇒ ∆AME = ∆AMF (cạnh huyền góc nhọn)

⇒ ME = MF (hai cạnh tương ứng)

Đúng(3)

P

Phongg

24 tháng 12 2023

a,
Xét tam giác ABC có:
+ AB = AC (giả thuyết)
+ Góc CAM = MAB (AM là phân giác góc BAC)
+ AM chung
⇒ 2 tam giác bằng nhau (cgc) (đpcm)

b,
Ta có:
+ Tam giác AMC = Tam giác ABM (theo câu a)
⇒ CM = MB (2 cạnh tương ứng) (1)
⇒ M là trung điểm BC (đpcm)
+ Mà AM là tia phân giác góc CAB (2)
+ Góc AMC = Góc AMB (3)
Từ (1), (2), (3).
⇒ AM ⊥ BC (t/c) (đpcm)

c,
Ta có:
Tam giác ACM = Tam giác ABM (theo câu A)
⇒ Góc ACM = Góc ABM (2 góc tương ứng)
Ta có:
+ ME ⊥ AB (giả thuyết)
⇒ Tam giác MEB vuông tại E
+ MF ⊥ AC (giả thuyết)
⇒ Tam giác CFM vuông tại F
Xét tam giác CFM vuông tại F và tam giác MEB vuông tại E có:
+ Góc ACM bằng góc ABM (chứng minh trên)
+ MC = MB (theo câu b)
⇒ Hai tam giác CFM = MEB (cạnh huyền góc nhọn)
⇒ ME = MF (hai cạnh tương ứng) (đpcm)

Đúng(1)

KP

Khánh phạm

24 tháng 12 2023

Cho tam giác ABC có AB=AC, AM là phân giác của góc BAC ( M thuộc BC ):

a, Chứng minh tam giác ABM= tam giác ACM

b, Chứng minh M là trung điểm của BC và AM vuông góc BC

c, Kẻ MF vuông góc AB ( F thuộc AB ) và ME vuông góc AC ( E thuộc AC ). Chứng minh EF // BC

#Toán lớp 7

1

LB

Lê Bảo Châu

24 tháng 12 2023

Cho △ABC có AB = AC, AM là phân giác của ∠BAC (M ∈ BC):

a, Chứng minh △ABM = △ACM.

b, Chứng minh M là trung điểm của BC và AM ⊥ BC.

c, Kẻ MF ⊥ AB (F ∈ AB) và ME ⊥ AC (E ∈ AC). Chứng minh EF // BC.

Giải:

a,

- Xét 2 △ABM và △ACM, có:

AB = AC (theo giả thiết)

∠CAM = ∠BAM (AM là phân giác của ∠BAC)

AM_cạnh chung

=> △ABM = △ACM (c.g.c)

b,

- Có △ABM = △ACM (chứng minh trên)

=> MC = MB (2 cạnh tương ứng)

=> M là trung điểm của BC

=> ∠AMC = ∠AMB (2 góc tương ứng)

mà 2 ∠AMC và ∠AMB kề bù

=> ∠AMC = ∠AMB = $\dfrac{180^o}{2}$ = 90^o

<=> AM ⊥ BC

c,

- Xét 2 △AEM và △AFM, có:

∠AEM = ∠AFM = 90^o

AM_cạnh chung

∠EAM = ∠FAM (AM là phân giác của ∠EAF)

=> △AEM = △AFM (cạnh huyền - góc nhọn)

=> AE = AF (2 cạnh tương ứng)

<=> △AEF cân tại A

$\hat{A E F} = \frac{180^{0} - \hat{A}}{2}$ ∠AEF = $\dfrac{180^o-\text{∠}EAF}{2}$ (số đo của một góc ở đáy trong △AEF cân tại A) (1)

Có △ABC cân tại A (AB = AC)

$\hat{A E F} = \frac{180^{0} - \hat{A}}{2}$ ∠ACB = $\dfrac{180^o-\text{∠}BAC}{2}$ (số đo của một góc ở đáy trong ΔABC cân tại A) (2)

Từ (1) và (2) suy ra ∠AEF = ∠ACB

mà ∠AEF và ∠ACB ở vị trí đồng vị

=> EF//BC

Đúng(1)

HD

Hương Đinh Thị Mai

6 tháng 5 2022

Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. a) Chứng minh ΔAMB = ΔAMC b) Từ M vẽ ME vuông góc với AB (E AB) và MF vuông góc với AC (F AC). Chứng minh: ME = MF c) So sánh ME với MC d) Kẻ BK là phân giác góc ABC (K AC); BK cắt AM tại I. Chứng minh CI là phân giác của góc...

Đọc tiếp

#Toán lớp 7

1

VT

Vũ Thảo Tiên

6 tháng 5 2022

a) Xét AMB và AMC

ta có: AB=AC ( vì ABC cân tại A )

BM=MC ( vì AM là đường trung tuyến )

AM: cạnh chung

Suy ra: AMB = AMC ( c.c.c )

Đúng(0)

KH

Khoa Hà

30 tháng 3 2022

Cho tam giác ABC có AB = AC = 5cm,BC = 6cm. Đường trung tuyến AM xuất phát từ đỉnh Acủa tam giác ABC

a, Chứng minh △AMB = △AMC và AM là tia phân giác của góc A

b, Chứng minh AM⊥BC

c, Tính độ dài các đoạn thẳng BM và AM

#Toán lớp 7

6

TC

TV Cuber

30 tháng 3 2022

thiếu , có hỏi j đou

Đúng(0)

ZT

Zero Two

30 tháng 3 2022

Đúng(1)

DB

dragon blue

21 tháng 5 2021

Cho tam giác ABC có AB = AC = 5cm, BC=6cm . đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABCa) Chứng minh $\Delta AMB=\Delta AMC$ và AM là tia phân của góc Ab) Chứng minh AM $\perp$ BCc) Tính độ dài các đoạn thẳng BM và AMd) Từ M vẽ ME $\perp$ AB ( E thuộc AB ) và MF $\perp$ AC ( F thuộc AC ) . Tam giác MEF là tam giác gì ? Vì saoai làm được mình cho 10000...

Đọc tiếp

#Toán lớp 7

3

TT

😈tử thần😈

21 tháng 5 2021

a) Xét ΔABC có AB=AC=5

=> ΔABC cân tại A

ta có AM là trung tuyến => AM là đường phân giác của góc A (tc Δ cân)

=>$\widehat{B}=\widehat{C}$(tc)

Xét ΔABM và ΔACM có

AB=AC gt

có AM là trung tuyến => BM=CM

$\widehat{B}=\widehat{C}$ (cmt)

=>ΔABM = ΔACM (cgc)

b) có ΔABC cân

mà AM là trung tuyến => AM là đường cao (tc Δ cân)

c) ta có AM là trung tuyến =>

M là trung điểm của BC

=> BM=CM=$\dfrac{BC}{2}=\dfrac{6}{2}=3$cm

Xét ΔABM có AM là đường cao => $\widehat{AMB}=$90^o

=> AM²+BM²=AB²

=> AM²+3²=5²

=> AM =4 cm

d) Xét ΔBME và ΔCMF có

$\widehat{MEB}=\widehat{MFC}=$90^o (ME⊥AB,MF⊥AC)

BM=CM (cmt)

$\widehat{B}=\widehat{C}$

=>ΔBME = ΔCMF (ch-cgv)

=>EM=FM( 2 góc tương ứng)

Xét ΔMEF có

EM=FM (cmt)

=> ΔMEF cân tại M

Đúng(2)

DB

dragon blue

21 tháng 5 2021

đố ai làm đc

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP