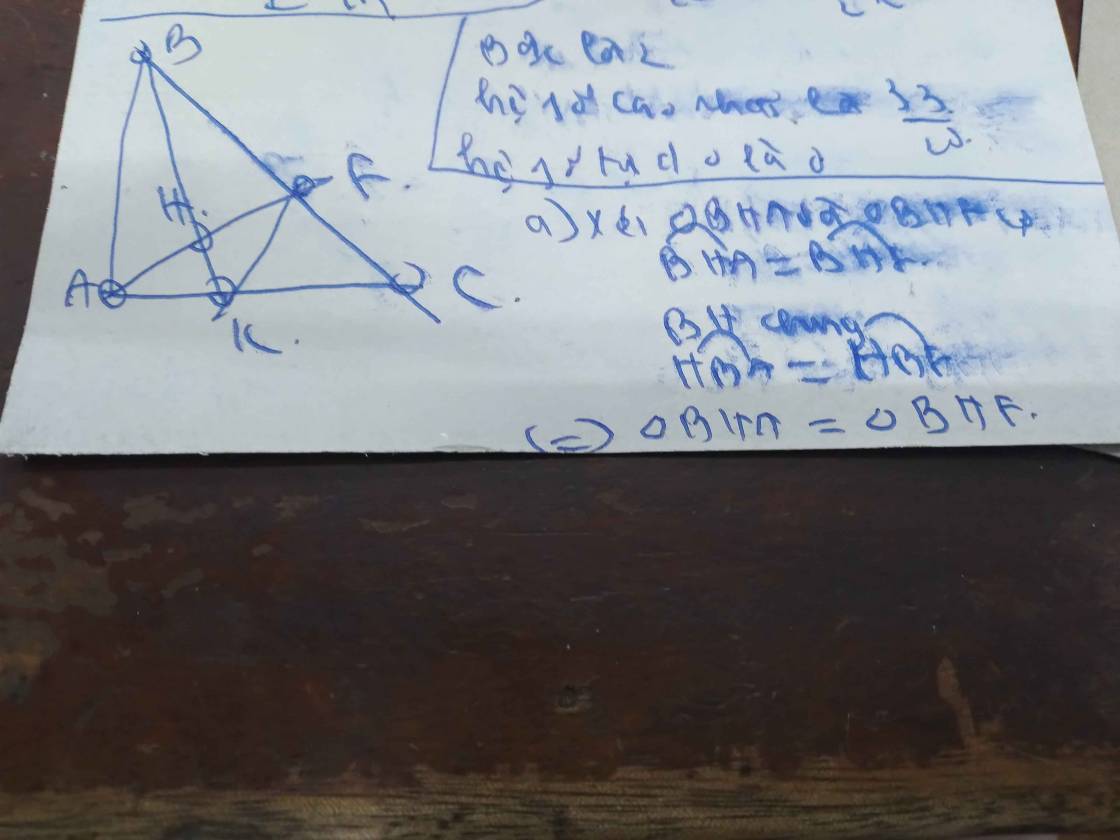
Bài 4: ( 2,5 điểm)
Cho ΔABC vuông tại A, kẻ phân giác BK của ![]() (K thuộc AC),
(K thuộc AC),
kẻ AE![]() tại H và E thuộc BC
tại H và E thuộc BC
a) Chứng minh: ΔBHA = ΔBHE.
b) Chứng minh: EK![]() .
.
c) Chứng minh: AK < KC.


a: Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
góc ABH=góc EBH
=>ΔBHA=ΔBHE
b: Xét ΔBAK và ΔBEK có
BA=BE
góc ABK=góc EBK
BK chung
=>ΔBAK=ΔBEK
=>góc BEK=90 độ
=>EK vuông góc BC
c: AK=KE
KE<KC
=>AK<KC