Em mong Thầy Cô, các anh chị, các bạn giúp em có đường lối làm câu c ạ. Em cảm ơn thầy cô và mọi người rất rất nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
2
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2021
Đặt \(\int f\left(x\right)dx=F\left(x\right)\Rightarrow\int\limits^{17}_1f\left(x\right)dx=F\left(17\right)-F\left(1\right)\)
Từ giả thiết:
\(2x.f\left(x^2+1\right)+\dfrac{f\left(\sqrt{x}\right)}{2\sqrt{x}}=2lnx\)
Lấy nguyên hàm 2 vế:
\(F\left(x^2+1\right)+F\left(\sqrt{x}\right)=2xlnx-2x+C\)
Thay \(x=4\):
\(F\left(17\right)+F\left(2\right)=16ln2-8+C\) (1)
Thay \(x=1\):
\(F\left(2\right)+F\left(1\right)=-2+C\) (2)
Trừ vế cho vế (1) cho (2):
\(F\left(17\right)-F\left(1\right)=16ln2-6\)
Vậy \(\int\limits^{17}_1f\left(x\right)dx=16ln2-6\)
HD
Hà Đức Thọ
Admin
7 tháng 6 2016
Cảm ơn bạn, do các giáo viên trên Hoc24 phải duyệt rất nhiều câu trả lời, nên không thể tránh khỏi sai sót, mong các bạn thông cảm. Hoc24 sẽ xem xét lại vấn đề này để phục vụ các bạn tốt hơn, cũng như tạo sân chơi công bằng cho các bạn!
20 tháng 11 2017
thường lúc chỉ thi thì thì dạng toán cần phải học là :
tính toán phân số , số thập phân
mấy bài toán đố về hình học
cuối cùng là tìm x
KH
7 tháng 7 2020
bạn phải học toán về hình hoc , tìm x , tỉ số phần trăm , phân só ,số thập phân và hỗn số ( cả toán đố của các dạng bài trên nữa)
DT
16 tháng 2 2022
program 06;
Uses crt;
Var
T:real
i;n:integer;
Begin
clrscr;
write('n=1');Readln(n);
T:=06
for i:=1 to n do
T:=\frac{1}{1}.2+\frac{1}{2}.5+\frac{1}{3}.8+\frac{1}{4}.11
write('T=06'; T);
readln;
end.
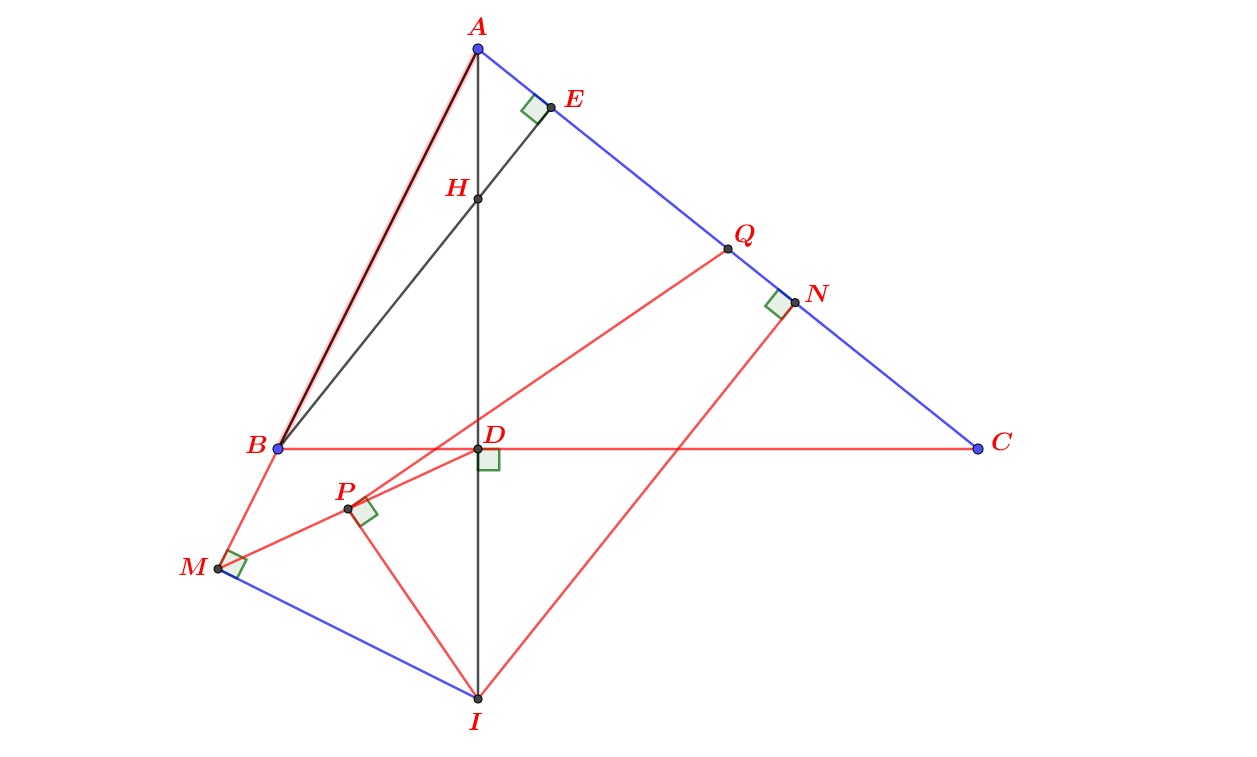
a) Do \(\widehat{EKA}=\widehat{EQA}=90^0\) nên \(AQKE\) nội tiếp. Suy ra \(\widehat{KQE}=\widehat{KAE}=\widehat{BCE}.\)
b) Tứ giác \(EDBK\) nội tiếp vì \(\widehat{EDB}=\widehat{EKB}=90^0\). Suy ra:
\(\widehat{EDK}=\widehat{EBK}=\widehat{ECA}\). Vậy thì \(DECN\) nội tiếp
Từ đó \(\widehat{END}=\widehat{ECB}=\widehat{EQK}\) và \(\widehat{DEN}=\widehat{ACB}=\widehat{QAK}=\widehat{KEQ}\)
Suy ra \(\Delta EDN~\Delta EKQ\). Vậy \(\frac{EN}{EQ}=\frac{ND}{QK}\Leftrightarrow EN.QK=ND.EQ\)
c) Ta có \(EF||AO\) vì cùng vuông góc với \(xy\). Do đó:
\(\widehat{EFB}=\widehat{BAO}=\widehat{EAC}=\widehat{EBI}\). Suy ra \(\Delta EIB~\Delta EBF\)
Suy ra \(\frac{EI}{EB}=\frac{EB}{EF}\Leftrightarrow\frac{EI}{EF}=\frac{EB^2}{EF^2}=\frac{BI^2}{FB^2}\) (1)
Ta lại có \(\widehat{FBI}=\widehat{KED},\widehat{BFI}=\widehat{EBI}=\widehat{EKD}\), cho nên \(\Delta FBI~\Delta KED\)
Suy ra \(\frac{BI^2}{FB^2}=\frac{ED^2}{EK^2}=\frac{S_{END}}{S_{EQK}}\) (2) do \(\Delta EDN~\Delta EKQ\)
Từ (1) và (2) ta suy ra \(\frac{S_{END}}{S_{EQK}}=\frac{EI}{EF}.\)