Chỉ em các bước giải với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi x là số mét tấm vải xanh ( x>18)
=> tấm vải đỏ = x - 18( mét) ( x> 18)
Sau khi cắt đi 1/2 tấm vải xanh và 1/5 tấm vải đỏ thì bằng nhau. Vậy, số tấm vải xanh còn lại là 1/2, số tấm vải đỏ còn lại là 4/5
=> ta có pt sau: \(\dfrac{x}{2}\)= \(\dfrac{4\left(x-18\right)}{5}\)
=> 5x = 8( x-18)
=> 5x = 8x - 144
=> - 3x = -144
=> 3x = 144
=> x = 48 ( thỏa)
=> tấm vải xanh dài 48m, tấm vải đỏ dài 30m
Đúng thì tim giúp mik nha. Thx bạn

\(\dfrac{BC}{x}=\dfrac{BC+6x}{BC}=>BC^2=BC.x+6x^2\)
\(=>6x^2+BC.x-BC^2=0\)
\(< =>6\left(x^2+\dfrac{1}{6}BCx-\dfrac{1}{6}BC^2\right)=0\)
\(=>x^2+\dfrac{1}{6}BCx-\dfrac{1}{6}BC^2=0\)
\(< =>x^2+2.\dfrac{1}{12}BC.x+\left(\dfrac{1}{12}BC^2\right)-\left(\dfrac{1}{12}BC\right)^2-\dfrac{1}{6}BC^2=0\)
\(< =>\left(x+\dfrac{1}{12}BC\right)^2-\left(\dfrac{5}{12}BC\right)^2=0\)
\(=>\left(x+\dfrac{1}{12}BC+\dfrac{5}{12}BC\right)\left(x+\dfrac{1}{12}BC-\dfrac{5}{12}BC\right)=0\)
\(< =>\left(x+\dfrac{1}{2}BC\right)\left(x-\dfrac{1}{3}BC\right)=0\)
\(=>\left[{}\begin{matrix}x+\dfrac{1}{2}BC=0\\x-\dfrac{1}{3}BC=0\end{matrix}\right.=>\left[{}\begin{matrix}BC=2x\\BC=3x\end{matrix}\right.\)

Câu 19:
\(=\dfrac{11x+x-18}{2x-3}=\dfrac{12x-18}{2x-3}=6\)
Câu 20:
\(=\dfrac{3x+5}{x\left(x-5\right)}+\dfrac{x-25}{5\left(x-5\right)}\)
\(=\dfrac{15x+25+x^2-25x}{5x\left(x-5\right)}=\dfrac{\left(x-5\right)^2}{5x\left(x-5\right)}=\dfrac{x-5}{5x}\)

\(5\sqrt{\dfrac{1}{2}}+\dfrac{1}{2}\sqrt{20}+\sqrt{5}\)
\(=\dfrac{5\sqrt{2}}{2}+\sqrt{5}+\sqrt{5}=\dfrac{5\sqrt{2}}{2}+2\sqrt{5}\)
\(=\dfrac{5\sqrt{2}}{2}+\dfrac{4\sqrt{5}}{2}=\dfrac{5\sqrt{2}+4\sqrt{5}}{2}\)
\(5\sqrt{\dfrac{1}{2}}+\dfrac{1}{2}\sqrt{20}+\sqrt{5}=\dfrac{5}{\sqrt{2}}+\dfrac{\sqrt{20}}{2}+\sqrt{5}=\dfrac{5\sqrt{2}+\sqrt{20}}{2}+\sqrt{5}=\dfrac{\sqrt{50}+\sqrt{20}}{\sqrt{4}}+\sqrt{5}=\dfrac{\sqrt{10}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{4}}+\sqrt{5}=\dfrac{\sqrt{5}\left(\sqrt{5}+\sqrt{2}\right)}{\sqrt{2}}+\sqrt{5}=\dfrac{5+\sqrt{10}+\sqrt{10}}{\sqrt{2}}=\dfrac{5+2\sqrt{10}}{\sqrt{2}}\)

Lời giải:
a.
$(5x-6)(1999^2+2.1999+1)=4.10^3$
$(5x-6)(1999+1)^2=(4.10^3)^2=4000^2$
$(5x-6).2000^2=4000^2$
$5x-6=\frac{4000^2}{2000^2}=2^2=4$
$5x=10$
$x=10:5=2$
b.
$(23545-7^5)x:[(8^4-4.10^3)^2-2478]=1$
$6738.x:6738=1$
$x=1$

b) 917-(417-65)
= 917- 352
= 565
c) 31-[26-(2017+35)]
= 31-[26-2052]
= 31- (-2026)= 31+2026= 2057
g) -418-{-218-[-118-(-131)]+2017}
= -418-{-218-[-118+131]+2017}
= -418-{-218-13+2017}
= -418-1786
= -2204
Các câu còn lại thì bạn làm tương tự nha!( nhân chia trước, cộng trừ sau, trong ngoặc làm trước ngoài ngoặc làm sau)





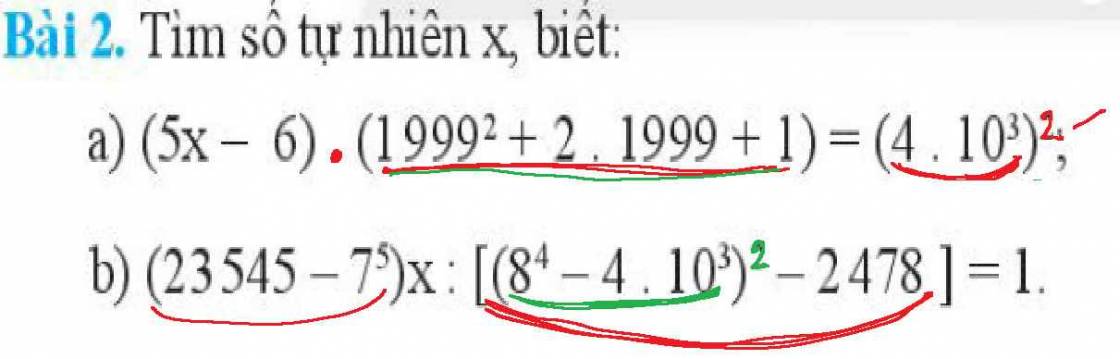


Nhìn trên hình bạn có thể thấy rõ các điểm đó là điểm (-1;1) và (2;4)
Nhưng trong trường hợp đề không cho hình thì ta làm như sau:
Phương trình hoành độ giao điểm của (P) và (d) là \(x^2=x+2\)\(\Leftrightarrow x^2-x-2=0\)(*)
Xét pt (*) có \(\Delta=\left(-1\right)^2-4.1.\left(-2\right)=9>0\)
Vậy pt (*) có 2 nghiệm phân biệt \(\orbr{\begin{cases}x_1=\frac{-\left(-1\right)+\sqrt{9}}{2.1}=2\\x_2=\frac{-\left(-1\right)-\sqrt{9}}{2.1}=-1\end{cases}}\)
Khi \(x=2\Rightarrow y=x+2=2+2=4\)
Khi \(x=-1\Rightarrow y=x+2=-1+2=1\)
Vậy ta tìm được đúng các điểm (-1;1) và (2;4)