Cho ΔABC vuông tại A(AB

D

DPKhanh

29 tháng 3 2022

Cho ΔABC vuông tại A(AB<AC) và D là trung điểm của BC. Từ D vẽ DE vuông góc với BC cắt AC tại Ea/ Chứng minh:ΔDEC đồng dạng với ΔABCb/Đường vuông góc với BC vẽ từ B cắt ta CA tại F. Chứng minh:BF2=FA.FCc/Gọi I là trung điểm của AB. Chứng minh:ΔFIB và Δ FDC đồng dạng.d/Hai đường thẳng FI và ED giao nhau tại M . Chứng minh:MC vuông góc FCchỉ cần c và d...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

11 tháng 7 2023

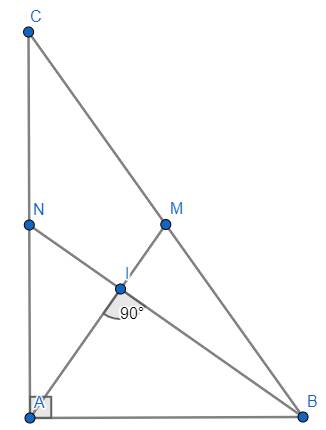
a: Xét ΔDEC vuông tại D và ΔABC vuông tại A có

góc C chung

=>ΔDEC đồng dạng với ΔABC

c:

Xét ΔBAF vuông tại A và ΔCBF vuông tại B có

góc F chung

=>ΔBAF đồng dạng với ΔCBF

=>BA/BC=FB/FC

IB/DC=BA/BC=FB/FC

Xét ΔFIB và ΔFDC có

góc FBI=góc FCD

IB/DC=FB/FC

=>ΔFIB đồng dạng với ΔFDC

Đúng(0)

DQ

Đặng Quốc Đạt

14 tháng 2 2022

Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP=√30cm,NP=√14 cmBài2:Cho ΔABC cân tại A. Biết AB=2cm. Tính BCBài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=6cm,HB=4cm,HC=9cmBài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=4cm,HB=2cm,HC=8cmBài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=4cm,HB=2cm,HC=8cm.Tính BC,AH,ACBài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=6cm,AC=8cm...

Đọc tiếp

#Toán lớp 7

2

NN

Nguyễn Ngọc Huy Toàn

14 tháng 2 2022

bạn đăng từng bài nhé

Đúng(0)

NL

Nguyễn Lê Phước Thịnh

14 tháng 2 2022

Bài 3:

\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)

BC=13cm

=>\(AC=3\sqrt{13}\left(cm\right)\)

Đúng(0)

LL

Ly Ly

2 tháng 10 2021

* Cho ΔABC vuông tại A có B= \(30^0\), AB=6cma. Giải ΔABCb. Vẽ đường cao AH và trung tuyến AM của ΔABC. Tính diện tích ΔAHM* Cho ΔABC vuông tại A có AB=3 cm, BC=5cm, đường cao AHa. Tính số đo góc B, Cb. Gọi AE là phân giác của góc A (E ∈ BC). Tính...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

2 tháng 10 2021

Bài 1:

a: Xét ΔBAC vuông tại A có

\(\widehat{B}+\widehat{C}=90^0\)

hay \(\widehat{C}=60^0\)

Xét ΔBAC vuông tại A có

\(AB=BC\cdot\sin60^0\)

\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)

\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)

Đúng(1)

DD

Diễm Đinh

5 tháng 7 2023

Cho ΔABC vuông tại B biết: BC=2a; góc A=45°: a) Tính độ dài cạnh AB; AC b) Kẻ BH vuông góc AC. Tính BH=? c) Tính diện tích ΔABC d) Tính chu vi ΔABC e) Tính bán kính đường tròn ngoại tiếp ΔABC

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

5 tháng 7 2023

a: ΔBAC vuông tại B có góc A=45 độ

nên ΔBAC vuông cân tại B

=>BA=BC=2a

AC=căn AB^2+BC^2=2a*căn 2

b: BH=BA*BC/AC=4a^2/2*a*căn 2=a*căn 2

c: S ABC=1/2*2a*2a=2a^2

d: C=2a+2a+2a*căn 2=4a+2a*căn 2

Đúng(0)

LT

Ly Thảo

10 tháng 5 2022

Cho tam giác ΔABC vuông tại A có AB=6cm,AC=10cm . Đường cao AH a)Chứng minh ΔABC / ΔABH b)Chứng minh AB²=BH.BC c)Tính BC,AH,BH

#Toán lớp 8

2

NL

Nguyễn Lê Phước Thịnh

10 tháng 5 2022

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

góc B chung

Do đó: ΔABC\(\sim\)ΔHBA

b: ta có: ΔABC\(\sim\)ΔHBA

nên BA/BH=BC/BA

hay \(BA^2=BH\cdot BC\)

Đúng(1)

NN

Nguyễn Ngọc Huy Toàn

10 tháng 5 2022

a.Xét tam giác ABC và tam giác HBA, có:

^B: chung

^BAC = ^BHA = 90 độ

Vậy tam giác ABC đồng dạng tam giác HBA (g.g)

b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)

\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)

c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)

(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)

\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)

Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)

Đúng(0)

HA

Hạ Ann

28 tháng 6 2021

Cho ΔABC vuông tại A. Chứng minh: Tan \(\dfrac{ABC}{2}=\dfrac{AB}{AB+BC}\)

#Toán lớp 9

2

NL

Nguyễn Lê Phước Thịnh

28 tháng 6 2021

Kẻ phân giác BK

Xét ΔABK vuông tại A có

\(\tan\widehat{ABK}=\dfrac{AK}{AB}\)

\(\Leftrightarrow\tan\dfrac{\widehat{ABC}}{2}=\dfrac{AK}{AB}\)(1)

Xét ΔABC có BK là đường phân giác ứng với cạnh AC(gt)

nên \(\dfrac{AK}{AB}=\dfrac{KC}{BC}\)(Tính chất đường phân giác)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AK}{AB}=\dfrac{KC}{BC}=\dfrac{AK+KC}{AB+BC}=\dfrac{AC}{AB+BC}\)(2)

Từ (1) và (2) suy ra \(\tan\dfrac{\widehat{ABC}}{2}=\dfrac{AC}{AB+BC}\)

Đúng(2)

HA

Hạ Ann

28 tháng 6 2021

Góc ABC nghenn mik ghii nhầm

Đúng(0)

NB

ngọc bảo

13 tháng 4 2022

Cho ΔABC vuông tại A có AB > AC, M là điểm tuỳ ý trên BC. Qua M kẻ Mx vuông góc với BC và cắt AB tại I cắt CA tại D.

a. Chứng minh ΔABC đồng dạng với ΔMDC

b. Chứng minh: BI.BA = BM.BC

c. Cho góc ACB = 60^o và S_ΔCDB = 60 cm². Tính S_ΔCMA.

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

1 tháng 7 2023

a: Xét ΔCMD vuông tại M và ΔCAB vuông tại A có

góc C chung

=>ΔCMD đồng dạng với ΔCAB

b: Xét ΔBMI vuông tại M và ΔBAC vuông tại A có

góc MBI chung

=>ΔBMI đồng dạng với ΔBAC

=>BM/BA=BI/BC

=>BM*BC=BA*BI

c: ΔCMD đồng dạng với ΔCAB

=>CM/CA=CD/CB

=>CM/CD=CA/CB

=>ΔCMA đồng dạng với ΔCDB

=>S CMA/S CDB=(CA/CB)^2=1/4

=>S CMA=15cm²

Đúng(0)

AH

Ánh Hoàng

31 tháng 5 2023

Cho ΔABC vuông tại A, AB = a. Các đường trung tuyến AM và BN vuông góc với nhau. Tính AB và BC theo a.

#Toán lớp 9

2

TM

Tô Mì

1 tháng 6 2023

Gọi \(I\) là giao điểm của \(AM\) và \(BN\Rightarrow IB=\dfrac{2}{3}BN;IN=\dfrac{1}{3}BN;AI=\dfrac{2}{3}AM;IM=\dfrac{1}{3}AM\)

\(\Delta ANB\) vuông tại \(A:AI^2=IB.IN\) \(\Rightarrow AI^2=\dfrac{2}{3}BN\cdot\dfrac{1}{3}BN=\dfrac{2}{9}BN^2\)

Ta cũng có trong \(\Delta ANB:AB^2=IB.BN\)

\(\Leftrightarrow a^2=\dfrac{2}{3}BN\cdot BN=\dfrac{2}{3}BN^2\Leftrightarrow BN^2=\dfrac{3}{2}a^2\)

Suy ra : \(AI^2=\dfrac{2}{9}BN^2=\dfrac{2}{9}\cdot\dfrac{3}{2}a^2=\dfrac{1}{3}a^2\).

Lại có : \(AI=\dfrac{2}{3}AM\Rightarrow AM^2=\dfrac{9}{4}AI^2=\dfrac{9}{4}\cdot\dfrac{1}{3}a^2=\dfrac{3}{4}a^2\)

\(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) của \(\Delta ABC\) vuông tại \(A\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC^2=4AM^2=4\cdot\dfrac{3}{4}a^2=3a^2\)

\(\Rightarrow BC=\sqrt{3a^2}=a\sqrt{3}\)

\(\Delta ABC\) vuông tại \(A\) có : \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)

\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{3a^2-a^2}=a\sqrt{2}\)

Vậy : \(AC=a\sqrt{2};BC=a\sqrt{3}\)

Đúng(1)

TM

Tô Mì

1 tháng 6 2023

Đúng(0)

HT

Hiếu Trung

30 tháng 4 2022

: Cho ΔABC vuông tại A có AB = 5cm, AC = 12cm.a/ Tính BC.b/ Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ΔABC = ΔADC.c/ Chứng minh : BCD cân tại C.d/ Vẽ đường thẳng qua A song song với BC cắt CD tại E, BE cắt AC tại G. Chứng minh : G làtrọng tâm của BDC. ( Dành cho các lớp 7 A, B, C)CÂU D THOI CX...

Đọc tiếp

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

30 tháng 4 2022

a: \(BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\)

b: Xét ΔABC vuông tại A và ΔADC vuông tại A có

AC chung

AB=AD

Do đó: ΔABC=ΔADC

c: Ta có: ΔABC=ΔADC

nên BC=DC

hay ΔCBD cân tại C

Đúng(0)

NB

Nguyễn Bảo Nam

11 tháng 1 2022

cho ΔABC vuông tại A. Trên tia đối tia AB, lấy điểm sao cho AD=AB

a. cm= ΔABC=ΔADC

b. Trên tia đối tia AC lấy điểm E sao cho AE=AC. Chứng minh BC//DE

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

11 tháng 1 2022

a: Xét ΔABC vuông tại A và ΔADC vuông tại A có

AB=AD

AC chung

Do đó: ΔABC=ΔADC

b: Xét tứ giác BCDE có

A là trung điểm của BD

A là trung điểm của CE

Do đó: BCDE là hình bình hành

Suy ra: BC//DE

Đúng(1)

NL

Nguyễn Lê Trân Châu

17 tháng 11 2021

cho ΔABC vuông tại A, biết AB=3cm, AC=4 cm, đường trung tuyến AD ( D ∈BC). Gọi M và N lần lượt là hình chiếu của D Trên AB và AC

a) tính BC, AD

b) chứng minh AD=MN

c) nếu ΔABC vuông cân tại A thì tứ giác BMNC là hình gì ? tại sao ?

#Toán lớp 8

1

NH

Nguyễn Hoàng Minh

17 tháng 11 2021

a. Pytago: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)

AD là trung tuyến ứng cạnh huyền BC nên \(AD=\dfrac{1}{2}BC=2,5\left(cm\right)\)

b. Vì \(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\) nên AMDN là hcn

Vậy AD=MN

c. ABC vuông cân A thì AD là trung tuyến cũng là p/g

Do đó AMDN là hình thoi(1)

Lại có D là trung điểm BC,DM//AC(⊥AB) nên M là trung điểm AB

Cmtt ta được N là trung điểm AC

Mà AB=AC nên AM=AC

Kết hợp (1) ta được AMDN là hình vuông

Đúng(3)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP