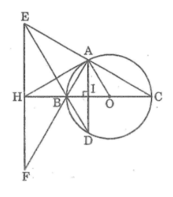
Cho (O) đường kính AB, dây cung AD > DB, kéo dài AD một đoạn DM = AD.
BM cắt (O) tại C, gọi H là giao điểm của AC và BD.
a) Chứng minh: AB = BM
b) Chứng minh: MH vuông góc AB tại
c) Gọi K là tâm đường tròn ngoại tiếp tứ giác DCHM. Chứng minh: DK là tiếp
tuyến của (O)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 7 2023
a: góc ADB=góc ACB=1/2*180=90 độ
=>BD vuông góc AM
Xét ΔBAM có
BD vừa là đường cao, vừa là trung tuyến
=>ΔBAM cân tại B
b: Xét ΔAMH có
HD,MC là đường cao
HD cắt MC tại B
=>B là trực tâm
=>AB vuông góc MH
12 tháng 3 2023
a: góc CMD=1/2*180=90 độ
góc CMF+góc CKF=180 độ
=>CKFM nội tiếp
b: Xét ΔDAF và ΔDMA có
góc DAF=góc DMA
góc ADF chung
=>ΔDAF đồng dạngvới ΔDMA
=>DA/DM=DF/DA
=>DA^2=DM*DF
31 tháng 7 2023
a: góc AMB=góc ACB=1/2*sđ cung AB=90 độ
=>AM vuông góc MB và AC vuông góc CB
góc BHK+góc BCK=180 độ
=>BHKC nội tiếp
góc EIA+góc EMA=180 độ
=>EIAM nội tiếp
b: Xét ΔAMK và ΔACM có
góc AMK=góc ACM(=góc ABM)
góc MAK chung
=>ΔAMK đồng dạng với ΔACM
=>AM/AC=AK/AM
=>AM^2=AK*AC
c: Xét ΔAIE vuông tại I và ΔACB vuông tại C có
góc IAE chung
=>ΔAIE đồng dạng với ΔACB
=>AI/AC=AE/AB
=>AI*AB=AC*AE
Xét ΔBIE vuông tại I và ΔBMA vuông tại M có
góc IBE chung
=>ΔBIE đồng dạng với ΔBMA
=>BI/BM=BE/BA
=>BI*BA=BM*BE
=>AE*AC+BM*BE=AB^2