Cho tứ giác ABCD có O là giao điểm của 2 đường chéo, AB=6cm, OA=8cm, OB=4cm, OD=6cm. Tính AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 6 2019
hình bn tự vẽ nha
cách giải, bn tham khảo ở đây nha
https://diendan.hocmai.vn/threads/cho-tu-giac-abc-co-o-la-giao-diem-2-duong-cheo.242620/
CM
21 tháng 8 2017
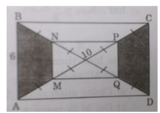
a) Ta có MN và PQ lần lượt là các đường trung bình của các tam giác AOB và COD mà AB // CD và AB = CD nên MN // PQ và MN = PQ
⇒ Tứ giác MNPQ là hình bình hành.
Tương tự NP // BC mà AB ⊥ BC nên MN ⊥ NP. Do đó MNPQ là hình chữ nhật.
Trong ΔABC ta có
Vậy SMNPQ = MN.PQ = 3.4 = 12 (cm2).
b)Dễ thấy ΔAOB = ΔCOD (c.c.c).
Tương tự ΔMON = ΔPOQ
Do đó: SAOB = SCOD và SMON = SPOQ.
⇒ SAOB - SMON = SCOD - SPOQ hay SAMNB = SCPQD.
2 tháng 3 2022
Chắc lớp 6 chưa học đến quá khó đâu , mình làm cách mang tính trực quan nhé
Ta có lục giác đều ABCDEG có các góc tạo bởi 2 cạnh kề nhau là 120 độ.
Khi lấy giao điểm O của các đường chéo đã chia hình thành 6 tam giác cân tại O và có góc ở đáy là 120: 2 =60 độ
Nên các tam giác AOB.BOC,COD,DOE,EOG,GOA là tam giác đều
=> AO=BO=CO=DO=OE=OG