Câu 23 , 24
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 10 2019
Đáp án là A
Ta có: M = 14 - 23 + (5 - 14) - (5 - 23) + 17 = 14 - 23 + 5 - 14 - 5 + 23 + 17
= (14 - 14) + (5 - 5) - (23 - 23) + 17 = 0 + 0 - 0 + 17 = 17
N = 24 - (72 - 13 + 24) - (72 - 13) = 24 - 72 + 13 - 24 - 72 + 13
= (24 - 24) - (72 + 72) + (13 + 13) = 0 - 144 + 26 = -118
Do đó M > N
17 tháng 1 2022
Câu 21: B
Câu 22: A
Câu 23: C
Câu 24: B
Câu 25: D
Câu 26: A
Câu 27: C
Câu 28: B
Câu 29: B
Câu 30: B
AH
Akai Haruma
Giáo viên
1 tháng 4 2021
Câu 22:
TXĐ: $(-\infty;0]\cup [2;+\infty)$
BPT \(\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x^2-2x\leq (x+1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -1\\ x\geq \frac{-1}{4}\end{matrix}\right.\Leftrightarrow x\geq \frac{-1}{4}\)
Kết hợp ĐKXĐ suy ra BPT có nghiệm $[\frac{-1}{4};0]\cup [2;+\infty)$
AH
Akai Haruma
Giáo viên
1 tháng 4 2021
Câu 23:
Theo công thức trung tuyến:
$CM^2=\frac{BC^2+AC^2}{2}-\frac{AB^2}{4}=\frac{23}{2}$
Áp dụng công thức Herong cho tam giác $ABC$:
$S_{ABC}=\sqrt{\frac{9}{2}(\frac{9}{2}-2)(\frac{9}{2}-3)(\frac{9}{2}-4)}=\frac{3\sqrt{15}}{4}$
$S_{BCM}=\frac{1}{2}S_{ABC}=\frac{3\sqrt{15}}{8}$
Áp dụng công thức: $S=\frac{abc}{4R}$ cho tam giác $BCM$ thì bán kính đường tròn ngoại tiếp tam giác là:
$R=\frac{BC.CM.BM}{4S_{BCM}}=\frac{4.\sqrt{\frac{23}{2}}.1}{\frac{3\sqrt{15}}{2}}=\frac{4\sqrt{690}}{45}$
17 tháng 2 2023
Câu 23:
Ta có: nH2O - nCO2 = nA = 0,23 - 0,14 = 0,09 (mol)
\(\Rightarrow\left\{{}\begin{matrix}\%n_A=\dfrac{0,09}{0,1}.100\%=90\%\\\%n_B=10\%\end{matrix}\right.\)
→ Đáp án: A
Câu 24:
nCO2 = nH2O ⇒ X là anken.
→ Đáp án: D
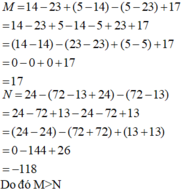
câu 21 22 23 24 giúp mình nha
23.
\(\left|2x-1\right|>\left|x-2\right|\Leftrightarrow\left(2x-1\right)^2>\left(x-2\right)^2\)
\(\Leftrightarrow4x^2-4x+1>x^2-4x+4\)
\(\Leftrightarrow x^2>1\Rightarrow\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\)
24.
Do \(x^2+2x+1>0;\forall x\ne-1\) nên với \(x\ne-1\) BPT trở thành:
\(x^2-4x+3\le0\Rightarrow1\le x\le3\)