Cứu mình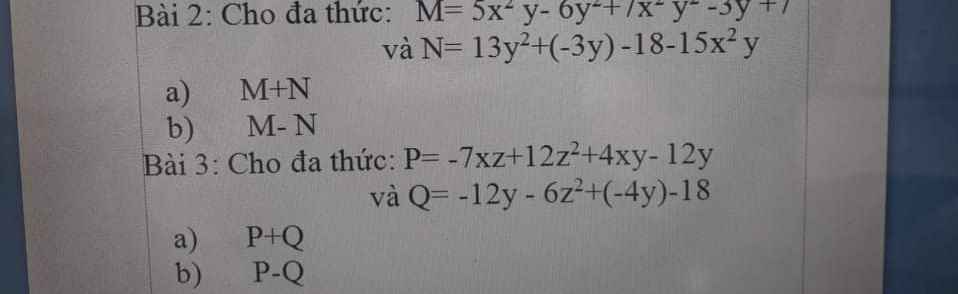
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\dfrac{1}{-2x^2+4x-2}=\dfrac{x-2}{-2\left(x-1\right)^2\left(x-2\right)}\\ \dfrac{1}{2x^2-6x+4}=\dfrac{x-1}{2\left(x-1\right)^2\left(x-2\right)}\)




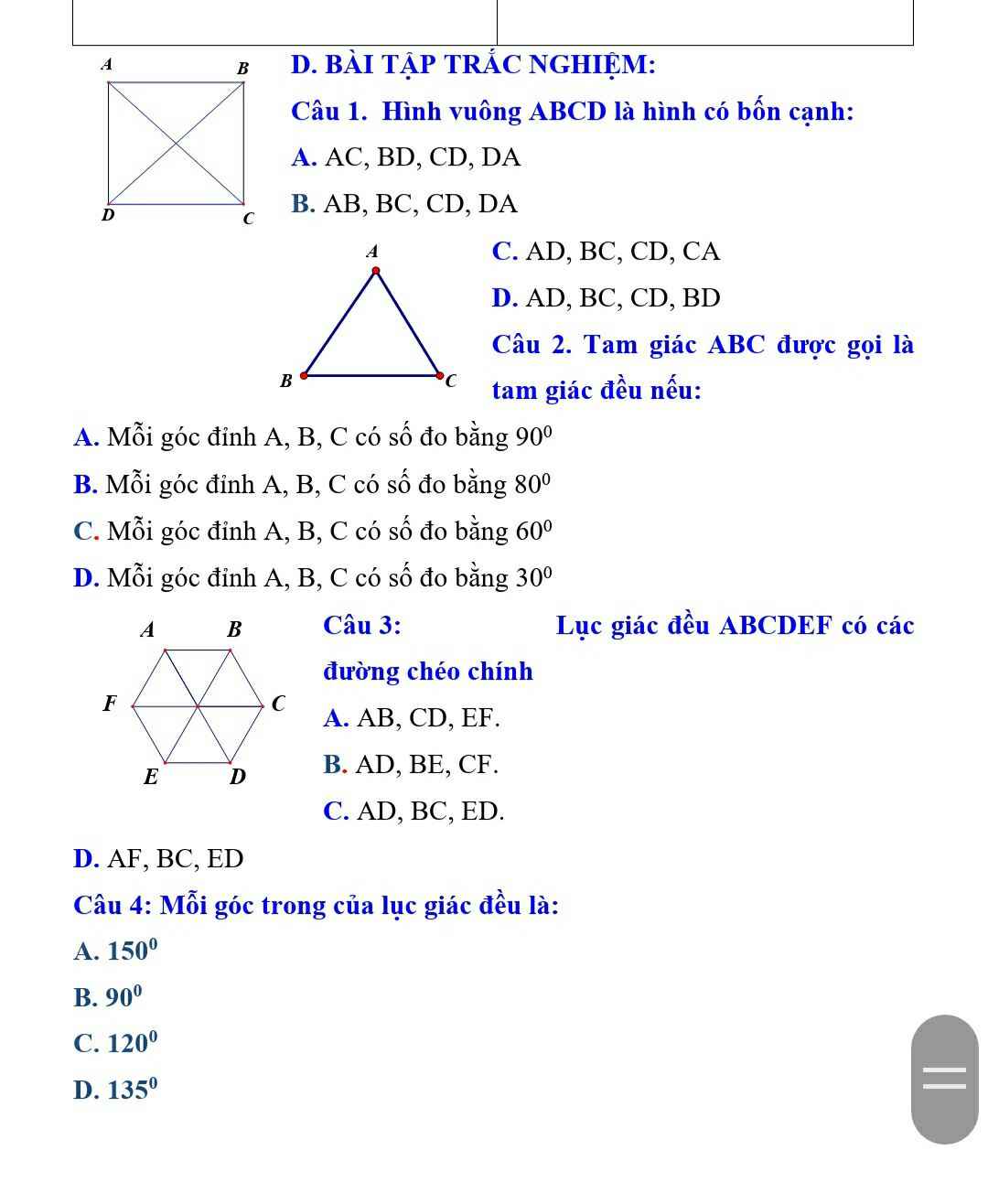
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: Ta có: ΔABD=ΔACE
nên AD=AE
=>BE=CD
Xét ΔEIB vuông tại E và ΔDIC vuông tại D có
EB=DC
\(\widehat{EBI}=\widehat{DCI}\)
Do đó: ΔEIB=ΔDIC
c: Ta có: ΔEIB=ΔDIC
nên IB=IC
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC

Gọi các phân số cần tìm là: \(\dfrac{a}{b}\) theo bài ra ta có:
\(\dfrac{a}{b}\) = \(\dfrac{a+2}{b\times2}\)
a.(b x 2) = (a + 2) x b
ab x 2 = ab + 2b
ab = 2b
a = 2
Ta có: \(\dfrac{2}{b}\) > \(\dfrac{1}{5}\) = \(\dfrac{2}{10}\)
⇒ b < 10 ⇒ b = 1; 2; 3; 4; 5; 6; 7; 8; 9
Vì \(\dfrac{2}{b}\) không phải là số tự nhiên nên b \(\in\) {3; 4; 5; 6; 7; 8; 9}
Bài 16:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + \(\dfrac{1}{7^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\)
\(\dfrac{1}{5^2}\) < \(\dfrac{1}{4.5}\) = \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\)
\(\dfrac{1}{6^2}\) < \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
............................
\(\dfrac{1}{100^2}\) < \(\dfrac{1}{99.100}\) = \(\dfrac{1}{99}\) - \(\dfrac{1}{100}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\)+...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) - \(\dfrac{1}{100}\) < \(\dfrac{1}{4}\) (1)
\(\dfrac{1}{5^2}\) > \(\dfrac{1}{5.6}\) = \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\)
\(\dfrac{1}{6^2}\) > \(\dfrac{1}{6.7}\) = \(\dfrac{1}{6}\) - \(\dfrac{1}{7}\)
...............................
\(\dfrac{1}{100^2}\) > \(\dfrac{1}{100.101}\) = \(\dfrac{1}{100}\) - \(\dfrac{1}{101}\)
Cộng vế với vế ta có:
\(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) + ... + \(\dfrac{1}{100^2}\) > \(\dfrac{1}{5}\) - \(\dfrac{1}{101}\)= \(\dfrac{96}{505}\) > \(\dfrac{96}{576}\) = \(\dfrac{1}{6}\) (2)
Kết hợp (1) và (2) ta có:
\(\dfrac{1}{6}\) < \(\dfrac{1}{5^2}\) + \(\dfrac{1}{6^2}\) +...+ \(\dfrac{1}{100^2}\) < \(\dfrac{1}{4}\) (đpcm)

Khi cộng vào tử số và mẫu số của phân số đã cho cùng một số tự nhiên thì hiệu của mẫu số và tử số không đổi và bằng:
11 - 2 = 9
Ta có sơ đồ: 
Theo sơ đồ ta có: Tử số lúc sau là: 9:(7-4)\(\times\) 4 = 12
Số cần thêm vào tử số và thêm vào mẫu số là: 12 - 2 = 10
ĐS...


`|2/3x-2/5|-1/2=1-(-2/3)|`
`|2/3x-2/5|-1/2=5/3`
`|2/3x-2/5|=13/6`
`[(2/3x-2/5=13/6),(2/3x-2/5=-13/6):}`
`[(x=77/20),(x=-53/20):}`
\(\left|\dfrac{2}{3}x-\dfrac{2}{5}\right|-\dfrac{1}{2}=1-\left(-\dfrac{2}{3}\right)\)
\(\Leftrightarrow\left|\dfrac{2}{3}x-\dfrac{2}{5}\right|-\dfrac{1}{2}=\dfrac{5}{3}\Leftrightarrow\left|\dfrac{2}{3}x-\dfrac{2}{5}\right|=\dfrac{13}{6}\)
TH1 : \(\dfrac{2}{3}x-\dfrac{2}{5}=\dfrac{13}{6}\Leftrightarrow\dfrac{2}{3}x=\dfrac{77}{30}\Leftrightarrow x=\dfrac{77}{20}\)
TH2 : \(\dfrac{2}{3}x-\dfrac{2}{5}=-\dfrac{13}{6}\Leftrightarrow\dfrac{2}{3}x=-\dfrac{53}{30}\Leftrightarrow x=-\dfrac{53}{20}\)





 Cứu mình gấp ạ!!! Mình sắp thi rồi!!!
Cứu mình gấp ạ!!! Mình sắp thi rồi!!!

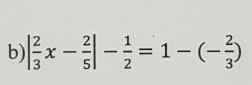
3:
a: P+Q
=12z^2-7xz+4xy-12y-12y-6z^2-4y-18
=6z^2-7xz+4xy-28y-18
b: P-Q
=12z^2-7xz+4xy-12y+12y+6z^2+4y+18
=18z^2-7xz+4xy+4y+18