Cho hình lập phương ABCD.A'B'C'D'. GÓC GIỮA HAI ĐƯỜNG THẲNG AD và A'C' là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 9 2017
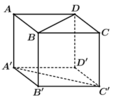
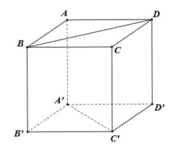
Ta có khoảng cách giữa hai đường thẳng chéo nhau BD và A'C' bằng khoảng cách giữa mặt phẳng song song (ABCD) và (A'B'C'D') thứ tự chứa BD và A'C' (hình vẽ). Do đó khoảng cách giữa hai đường thẳng BD và A'C' bằng a Chọn A.
CM
18 tháng 2 2019
Chọn A.
Ta có
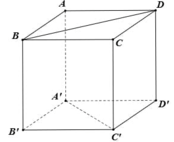
A B C D / / A ' B ' C ' D B D ⊂ A B C D A ' C ' ⊂ A ' B ' C ' D ' ⇒ d B D ; A ' C ' = d A B C D ; A ' B ' C ' D ' = A A ' = a
CM
22 tháng 8 2017
Ta có: d ( BD;A'C' ) = d ( BD;( A'B'C'D' )) = d ( B;( A'B'C'D' )) = BD' = a
Đáp án cần chọn là B
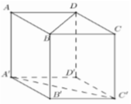
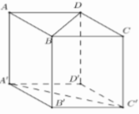
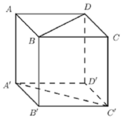
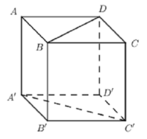
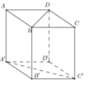
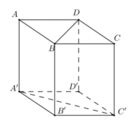
Do \(AC||A'C'\Rightarrow\widehat{\left(AD;A'C'\right)}=\widehat{\left(AD;AC\right)}=\widehat{CAD}=45^0\)