Mình cần gấp bạn nào giúp mik với :((((((((((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f,=\left(5^2+3\right):7=28:7=4\\ g,=7^2-9+8\cdot25=49-9+200=240\\ h,=600+72+18=690\\ i,=5^2+5-20=10\\ j,=45-28+83=100\)

\(2A=\frac{4}{1.5}+\frac{6}{5.11}+\frac{8}{11.19}+\frac{10}{19.29}+\frac{12}{29.41}\)
\(=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{11}+\frac{1}{11}-\frac{1}{19}+...+\frac{1}{29}-\frac{1}{41}=1-\frac{1}{41}=\frac{40}{41}\)
\(\Rightarrow A=\frac{20}{21}\)
\(3B=\frac{3}{1.4}+\frac{6}{4.10}+\frac{9}{10.19}+\frac{12}{19.31}=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{10}+\frac{1}{10}-\frac{1}{19}+\frac{1}{19}-\frac{1}{31}\)
\(=1-\frac{1}{31}=\frac{30}{31}\)
\(\Rightarrow B=\frac{10}{31}=\frac{20}{62}<\frac{20}{41}\)
Do đó $A>B$
Ta có: \(A=\dfrac{2}{1.5}+\dfrac{3}{5.11}+\dfrac{4}{11.19}+\dfrac{5}{19.29}+\dfrac{6}{29.41}\)
\(2A=1-\dfrac{1}{5}+\dfrac{1}{5}+...+\dfrac{1}{29}-\dfrac{1}{41}\)
\(2A=1-\dfrac{1}{41}=\dfrac{40}{41}\)
\(A=\dfrac{20}{41}\)
Lại có: \(B=\dfrac{1}{1.4}+\dfrac{2}{4.10}+\dfrac{3}{10.19}+\dfrac{4}{19.31}\)
\(3B=\dfrac{3}{1.4}+\dfrac{6}{4.10}+\dfrac{9}{10.19}+\dfrac{12}{19.31}\)
\(3B=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{10}+...+\dfrac{1}{19}-\dfrac{1}{31}\)
\(3B=1-\dfrac{1}{31}=\dfrac{30}{31}\)
\(B=\dfrac{10}{31}\)
Vì \(\dfrac{20}{41}>\dfrac{10}{31}\) nên...

\(\frac{x}{468}=-\frac{7}{13}\times\frac{5}{9}\)
\(\Leftrightarrow\frac{x}{468}=-\frac{35}{117}\)
\(\Leftrightarrow x.117=-35\times468\)
\(\Leftrightarrow x.117=-14976\)
\(\Leftrightarrow x=-128\)
Vậy \(x=-128\)
x/468=-7/13x 5/9
x/468=-35/117
=>x.117=-35.468
=>x.117=-16380
x=-16380:117
x=-140
Vậy x= -140.

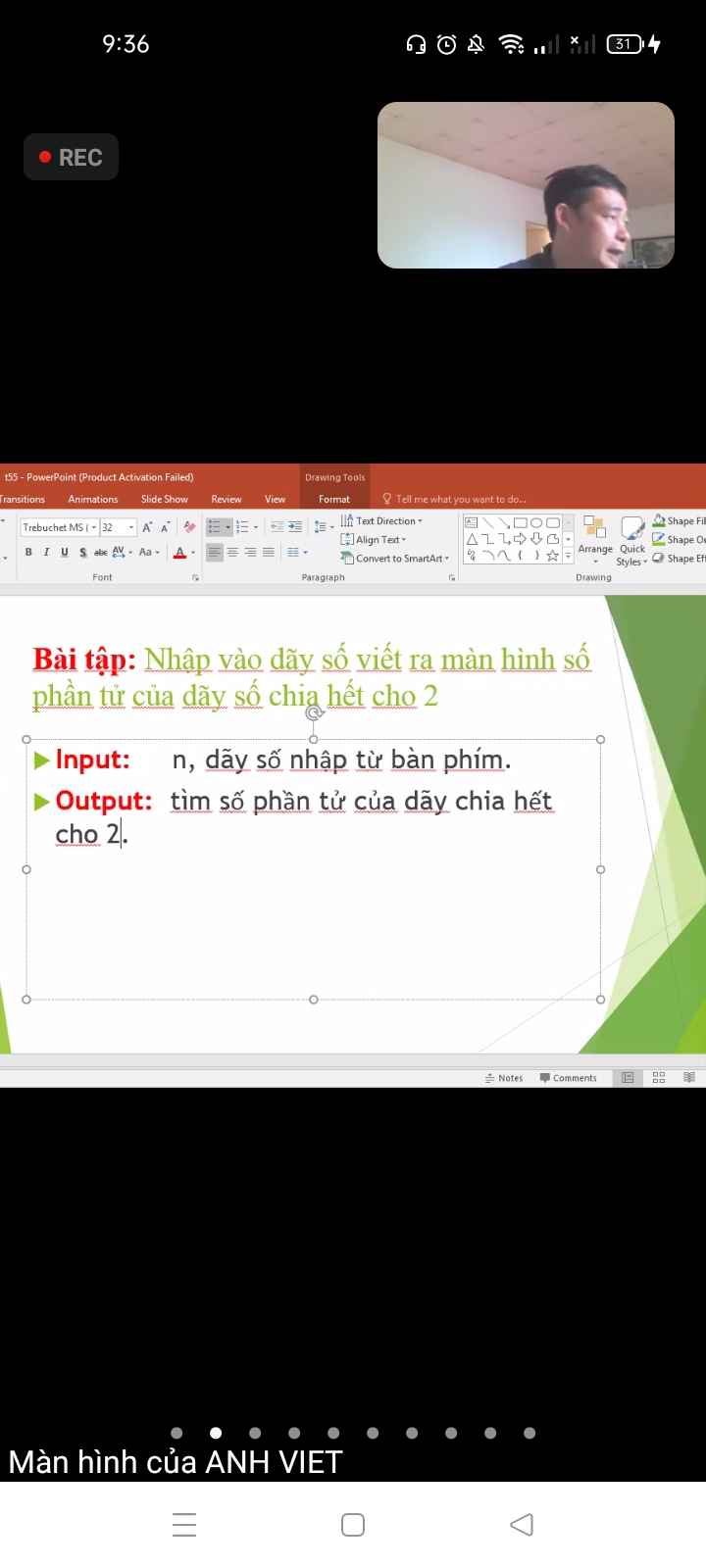
#include <bits/stdc++.h>
using namespace std;
long long x,i,n,dem;
int main()
{
cin>>n;
dem=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x%2==0) dem++;
}
cout<<dem;
return 0;
}

từ bác đầu tiên là: bác bỏ. Nghĩa của nó là ko đồng ý với ý kiến của người đưa ra
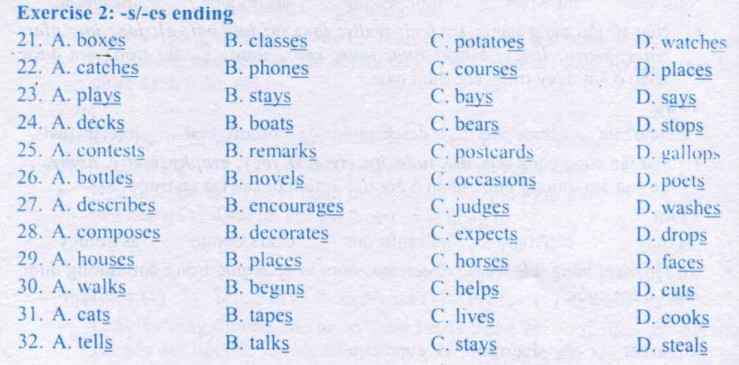
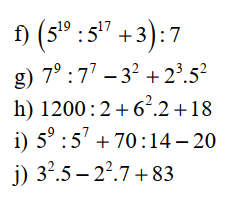 giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim
giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim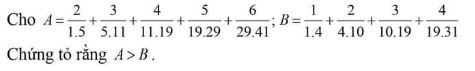

a: Xét ΔEDM và ΔEBA có
góc EDM=góc EBA
góc DEM=góc BEA
=>ΔEDM đồng dạng với ΔEBA
=>ED/EB=DM/BA
=>10/BA=8/6=4/3
=>BA=7,5cm
b: Xét ΔFAB và ΔFCM có
góc FAB=góc FCM
góc AFB=góc CFM
=>ΔFAB đồng dạng với ΔFCM
=>FB/FM=FA/FC=AB/CM=AB/DM
=>FB/FM=EA/EM
=>FE//AB