Cho tam giác ABC vuông tại A (AC > AB). Trên đoạn AC lấy điểm M và vẽ đường tròn đường kính MC. Tia BM cắt đường tròn tại D. Đường thẳng AD cắt đường tròn tại S.
a. C/m: ABCD là tứ giác nội tiếp.
b. C/m: CA là phân giác của góc SCB.
c. Gọi H là giao điểm thứ hai của đường tròn đường kính MC với BC. C/m: các đường thẳng AB; MH; CD đồng qui.
d. Biết CM = a; Cˆ = 300. Tính diện tích hình quạt OMmH ( với cung MmH là cung nhỏ.)
e. C/m : M là tâm đường tròn nội tiếp tam giác ADH.
f. ABˆC = 720 ; BCˆD = 73o tính các góc của tam giác AHD
g. Trong trường hợp DA là tiếp tuyến của đường tròn đường kính MC thì M ở vị trí nào?

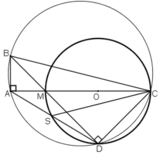
 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
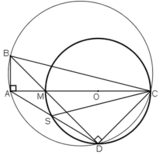
 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
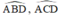 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 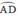
 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 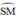
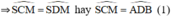
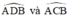 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 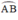
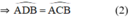

a: góc MDC=1/2*sđ cung MC=90 độ
=>góc BDC=90 độ
Xét tứ giác ABCD có
góc CAB=góc CDB=90 độ
=>ABCD nội tiếp
b: ABCD nội tiếp
=>góc BCA=góc BDA
=>góc BCA=góc SCA
=>CA là phân giác của góc SCB
c: Gọi N là giao của MH với AB
góc MHC=1/2*180=90 độ
=>NH vuông góc BC
Xét ΔCBN có
NH,CA là đường cao
NH cắt CA tại M
=>M là trực tâm
=>BM vuông góc CN
=>C,D,N thẳng hàng
=>MH,CD,BA đồng quy