biết \(\dfrac{MN}{HK}\)=\(\dfrac{3}{5}\) và MN = 9cm, độ dài đoạn HK là
a. 36cm
b. 27cm
c. 12cm
d. 15cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LL
7
Những câu hỏi liên quan
CM
25 tháng 7 2019
Đáp án là B
Vì H là trung điểm của đoạn thẳng MN nên HN = (1/2)MN = (1/2).5 = 2,5cm.
Vì K là trung điểm của đoạn thẳng NP nên NK = (1/2)NP = (1/2).9 = 4,5cm.
Ta có N nằm giữa hai điểm M và P nên NM và NP là hai tia đối nhau (1)
Vì H là trung điểm của MN nên H thuộc NM (2)
Vì K là trung điểm của NP nên K thuộc NP (3)
Từ (1), (2), (3) suy ra N là điểm nằm giữa hai điểm H và K.
⇒ HN + NK = HK = 2,5 + 4,5 = HK ⇒ HK = 7cm
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 6 2021
\(\dfrac{MN}{MP}=\dfrac{3}{4}\Rightarrow MN=\dfrac{3}{4}MP\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{MI^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\)
\(\Leftrightarrow\dfrac{1}{\left(\dfrac{48}{5}\right)^2}=\dfrac{1}{\left(\dfrac{3}{4}MP\right)^2}+\dfrac{1}{MP^2}\)
\(\Rightarrow MP^2=\dfrac{20736}{625}\Rightarrow MP=\dfrac{144}{25}\)
\(\Rightarrow MN=\dfrac{3}{4}MP=\dfrac{108}{25}\)
\(NP=\sqrt{MN^2+MP^2}=\dfrac{36}{5}\)
b. Áp dụng hệ thức lượng:
\(MP^2=IP.NP\Rightarrow IP=\dfrac{MP^2}{NP}=\dfrac{576}{125}\)
\(S_{MIP}=\dfrac{1}{2}IP.MI=\dfrac{13824}{625}\)
CM
28 tháng 4 2018
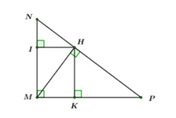
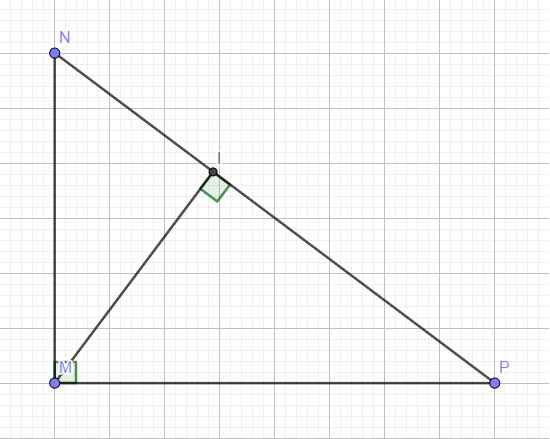
Xét tứ giác MIHK ta có M ^ = I ^ = K ^ = 90 0
=> MIHK là hình chữ nhật (dhnb)
=> HI = ML = 6cm
Áp dụng định lý Pytago cho MHK vuông tại K ta có:
Áp dụng hệ thức lượng trong MHP vuông tại H có đường cao HI ta có:
Áp dụng định lý Pytago cho MNP vuông tại N ta có:
Đáp án cần chọn là: B
21 tháng 1 2023
a: AC=AB=15cm
MC=15-9=6cm
Xét ΔBACcó BM là phân giác
nên AM/AB=MC/BC
=>6/BC=9/15=3/5
=>BC=10cm
b: Xét ΔABM và ΔACN có
góc ABM=góc ACN
AB=AC
góc BAM chung
=>ΔABM=ΔACN
=>AM=AN
Xét ΔABC có AN/AB=AM/AC
nên MN//BC
c: Xét ΔABC cóMN//BC
nên AM/AC=MN/BC
=>MN/10=9/15=3/5
=>MN=6cm
11 tháng 7 2022
a: Đặt MN/3=MK/4=k
=>MN=3k; MK=4k
Theo đề, ta có: \(MN^2+MK^2=NK^2\)
\(\Leftrightarrow25k^2=100\)
=>k=2
=>MN=6cm; MK=8cm
b: Xét ΔMNK vuông tại M có MH là đườg cao
nên \(MN^2=NH\cdot NK\)
\(\Leftrightarrow NH^2+32HK-900=0\)
=>NH=18(cm)
=>NK=18+32=50cm
\(MK=\sqrt{50^2-30^2}=40\left(cm\right)\)
\(MN=\dfrac{30\cdot40}{50}=24\left(cm\right)\)
D
D