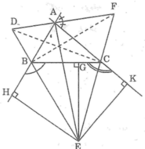
Trong mặt phẳng Oxy , cho tam giác ABC có D là chân đường phân giác trong góc B, E là trung điểm BD . Đường thẳng CE cắt phân giác ngoài góc B tại F. Viết phương trình đường thẳng BC biết B(5;1) , F(4;3) và đường thẳng qua A có phương trình là x +2y - 18 =0 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 1 2016
: a/ góc ABD=góc ABF=gòc By=60 độ. Xét tam giác ABD có 2 tia phân giác ngoài tại đỉnh A,B cắt nhau tại F , Suy ra DF là tia F B phân giác ABD. Vậy góc ADF=góc BDF b/ Xét tam giác DBC có tia phân giác góc C và tia phân giác ngoài tại điỉnh B,cắt nhau tại E. Suy ra DE là tia phân giác ngoài của ADˆB . A D C Tia DE và DF đều là tia phân giác của góc ADB . => Nên 3 điểm D,E,F thẳng hàng.
18 tháng 5 2021
Gọi AF giao BC tại G. Theo ĐL Thales thì \(\frac{FA}{FG}=\frac{ED}{EB}=1\), suy ra F là trung điểm AG
Dễ thấy tam giác ABG cân tại B,do đó AG vuông góc BF
Đường thẳng AG: đi qua \(F\left(4;3\right)\), VTPT \(\overrightarrow{FB}=\left(1;-2\right)\)\(\Rightarrow AG:x-2y+2=0\)
Xét hệ \(\hept{\begin{cases}x+2y-18=0\\x-2y+2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=8\\y=5\end{cases}}\Rightarrow A\left(8;5\right)}\)
Vì F là trung điểm AG nên \(G\left(0;1\right)\)\(\Rightarrow\overrightarrow{GB}=\left(5;0\right)\)=> VTPT của BC là \(\left(0;1\right)\)
\(\Rightarrow BC:x-1=0\). Vậy \(d\left(O;BC\right)=1.\)
CM
16 tháng 7 2019
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.
tên thật là Mai Thúc Loan (梅叔鸞), là vị vua người Việt thời Bắc thuộc, anh hùng dân tộc, người lãnh đạo cuộc khởi nghĩa chống lại sự chiếm đóng của nhà Đường ở Việt Nam vào đầu thế kỉ thứ 8.