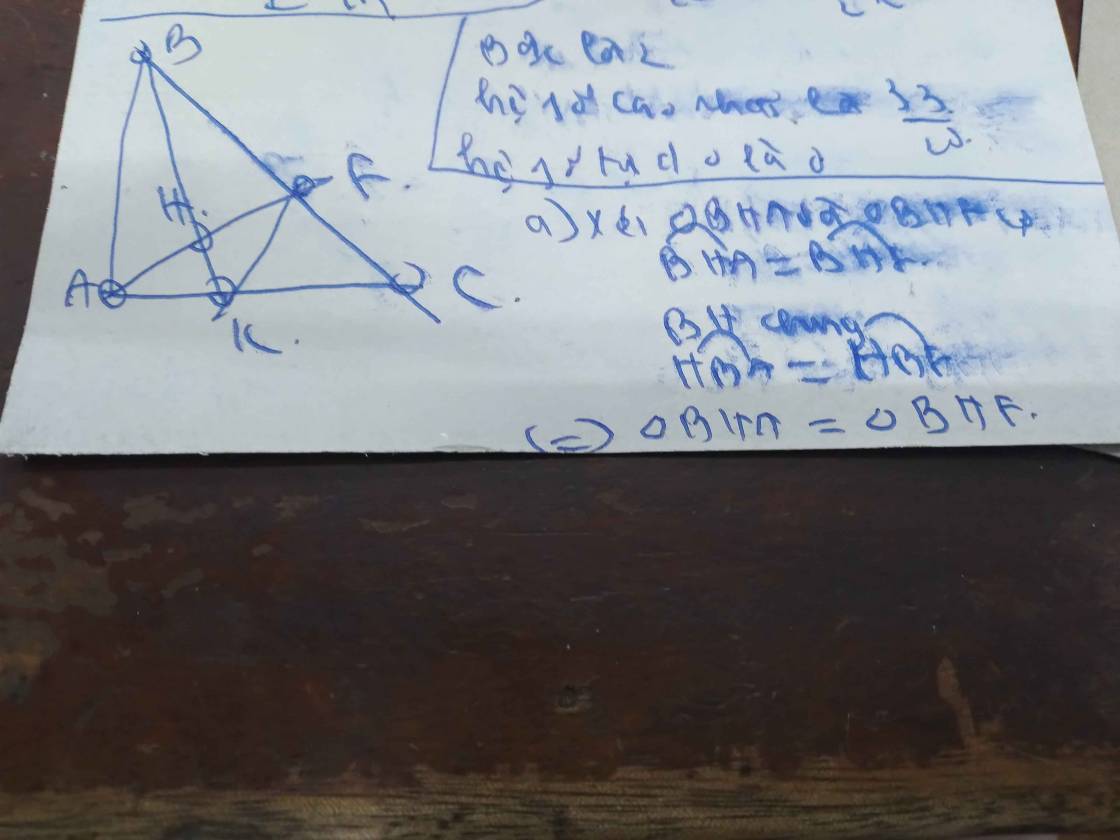
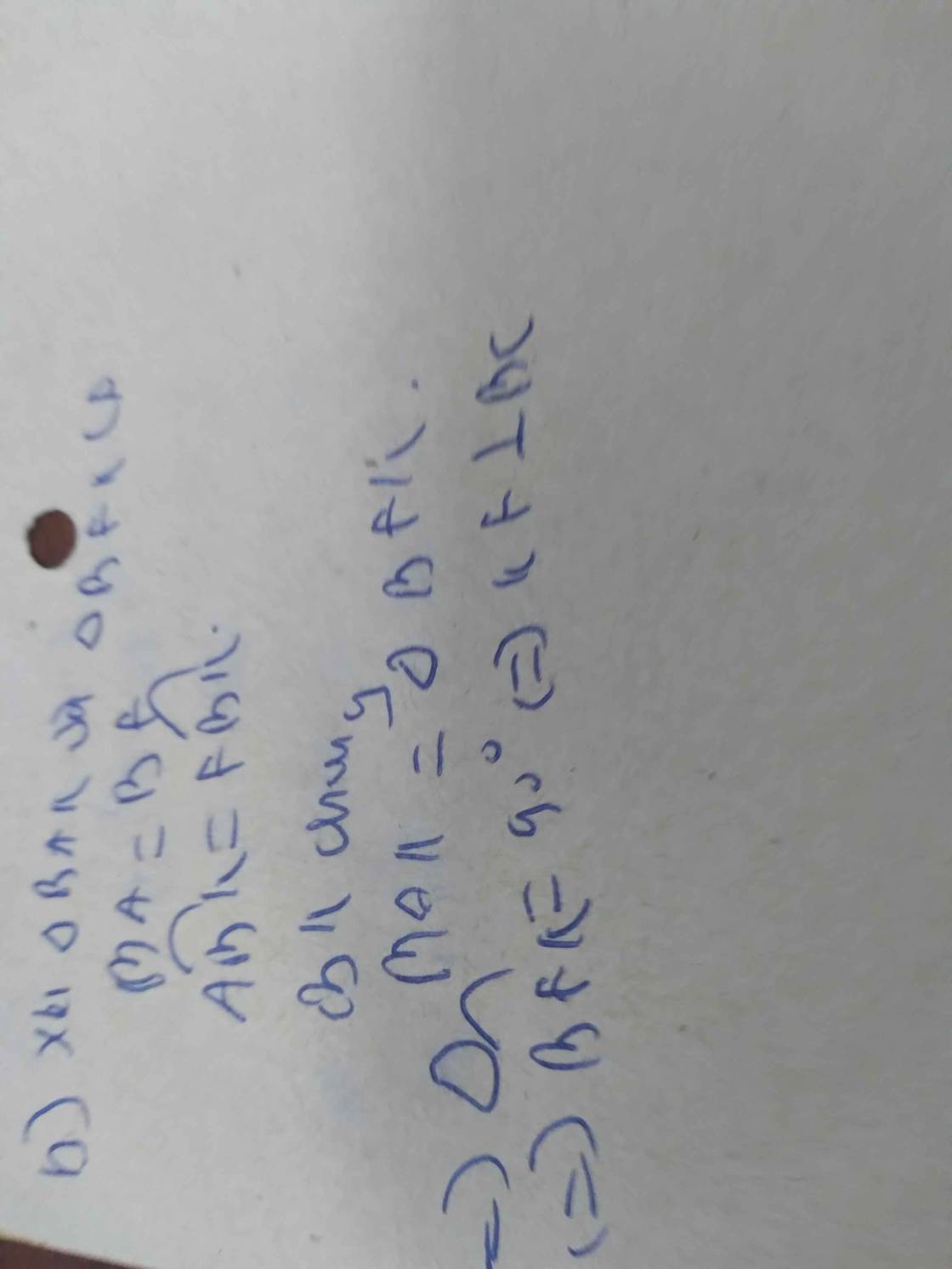cho tam giác ABC vuông tại A,kẻ phân giác BK của góc B(K thuộc AC),kẻ AE vuông góc với BK tại H và E thuộc BC a.chứng minh:AK<KC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Xét ΔBHA vuông tại H và ΔBHE vuông tại H có
BH chung
góc ABH=góc EBH
=>ΔBHA=ΔBHE
c: ΔBHA=ΔBHE
=>BA=BE
Xét ΔBAK và ΔBEK có
BA=BK
góc ABK=góc EBK
BK chung
=>ΔBAK=ΔBEK
=>góc BEK=góc BAK=90 độ
=>EK vuông góc bC
d: AK=KE
KE<KC
=>AK<KC

a, tam giác vuông CHF=CHE (c.g.c) => CF=CE => Tam giác CEF cân tại C
gọi O là giao điểm của Ak và BF
tam giác vuông ABF=KBF ( cạnh huyền góc nhọn ) => BA=BK
BA=BK; BO chung; ABO=KBO ( BF phân giác ) => tam giác ABO=KBO (c.g.c)=> AOB=KOB ở vị trí kề bù AOB+KOB=180
=> AOB=KOB=90=> BF vuông AK
=> AK//HC ( cùng vuông BF)
b, tam giác vuông ABF=KBF => AF=FK
cạnh huyền FC > FK => FC > FA
c, gọi D là giao điểm AB;CH
tam giác BDC có BH ; AC là 2 đường cao cắt nhau tạo F
mà FK vuông BC nên DK là đường cao thứ 3 trong tam giác này
=> Ba đường thẳng CH, FK,AB đồng quy

Có gì khong hiểu hỏi lại cj nhé:
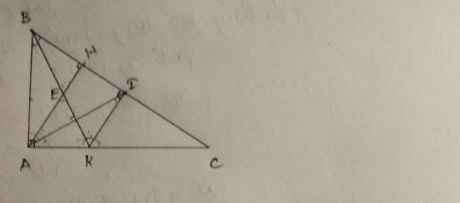
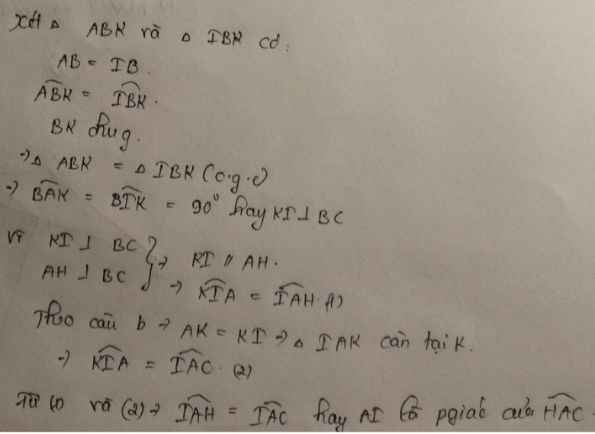
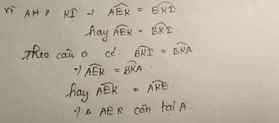
a, b ,c lần lượt từ trên xuống.

a) Xét ∆ ABK và ∆IBK có:
+\(\widehat{ABK}=\widehat{KBI}\)(gt)
+BK chung
+\(\widehat{BAK}=\widehat{BIK}\left(=90^o\right)\)
\(\Rightarrow\)∆ABK=∆IBK(ch-gnhon)
b) Ta có: \(\left\{{}\begin{matrix}KI\perp BC\left(gt\right)\\AD\perp BC\left(gt\right)\end{matrix}\right.\)
Do đó: KI//AD
\(\Rightarrow\widehat{DAI}=\widehat{AIK}\)(2 góc SLT) (1)
Ta có ∆ABK=∆IBK(cmt)
nên KA=KI (2 cạnh tương ứng)
Xét ∆KAI cân tại K
\(\Rightarrow\widehat{KAI}=\widehat{KIA}\)(2 góc đáy) (2)
Từ (1) và (2)\(\Rightarrow\widehat{DAI}=\widehat{KAI}\Leftrightarrow\widehat{DAI}=\widehat{IAC}\)
=> AI là tia pgiac(đpcm)

b) Ta có: KI\(\perp\)BC(gt)
AH\(\perp\)BC(gt)
Do đó: KI//AH(Định lí 1 từ vuông góc tới song song)
Suy ra: \(\widehat{HAI}=\widehat{KIA}\)(hai góc so le trong)(1)
Ta có: ΔABK=ΔIBK(cmt)
nên KA=KI(hai cạnh tương ứng)
Xét ΔKAI có KA=KI(cmt)
nên ΔKAI cân tại K(Định nghĩa tam giác cân)
Suy ra: \(\widehat{KAI}=\widehat{KIA}\)(hai góc ở đáy)(2)
Từ (1) và (2) suy ra \(\widehat{HAI}=\widehat{KAI}\)
\(\Leftrightarrow\widehat{HAI}=\widehat{CAI}\)
Suy ra: AI là tia phân giác của \(\widehat{HAC}\)(Đpcm)
a) Xét ΔABK vuông tại A và ΔIBK vuông tại I có
BK chung
\(\widehat{ABK}=\widehat{IBK}\)(BK là tia phân giác của \(\widehat{ABI}\))
Do đó: ΔABK=ΔIBK(Cạnh huyền-góc nhọn)