22x+22x+1+22x+2+...+22x+1918=21923-24
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
NA
2

NT
0

PN
1

15 tháng 7 2022
Câu 1:
\(\Leftrightarrow2\cdot\left(1-\sin^22x\right)+5\sin2x-4=0\)
\(\Leftrightarrow-2\sin^22x+5\sin2x-2=0\)
\(\Leftrightarrow\left(\sin2x-2\right)\left(2\sin2x-1\right)=0\)
\(\Leftrightarrow\sin2x=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\Pi}{6}+k2\Pi\\2x=\dfrac{5}{6}\Pi+k2\Pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{12}+k\Pi\\x=\dfrac{5}{12}\Pi+k\Pi\end{matrix}\right.\)
VM
0

TK
1

18 tháng 8 2020
bạn ơi, cho mình hỏi là tại sao từ bước 2 xuống bước 3, tử sin22x-2 lại đổi thành 2-sin22x vậy ạ
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2020
Nhân cả tử và mẫu với -1 thôi bạn
\(=\frac{2-sin^22x}{4cos^2x\left(1-sin^2x\right)}=\frac{2-sin^2x}{4cos^2x.cos^2x}\)
SB
0

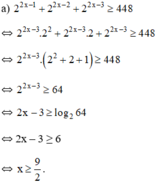
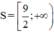
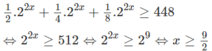
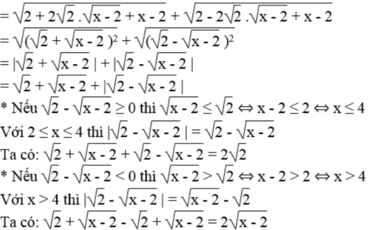
Đặt \(A=2^{2x}+2^{2x+1}+...+2^{2x+1918}\)
=>\(2\cdot A=2^{2x+1}+2^{2x+2}+...+2^{2x+1919}\)
=>\(A=2^{2x+1919}-2^{2x}\)
Theo đề, ta có; \(2^{2x+1919}-2^{2x}=2^{1923}-2^4\)
=>\(2^{2x}\cdot\left(2^{2019}-1\right)=2^4\left(2^{2019}-1\right)\)
=>2x=4
=>x=2