gải chi tiết dúp mình nha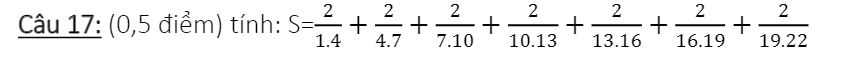 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PH
5
28 tháng 11 2017
= 100 - 570 - 234 - 430
= ( 100 - 570 - 430 ) - 234
= ( 100 - 1000 ) - 234
= - 900 - 234
= - 1134
Giúp Mình Gải chi tiết đc ko ? Mình cần gấp
23 tháng 1 2022
\(B=\left(\dfrac{1}{9}-\dfrac{5}{7}\right)+\dfrac{3}{6}+\left(\dfrac{-12}{17}+\dfrac{-1}{2}\right)+\dfrac{5}{9}.\)
\(B=\dfrac{1}{9}-\dfrac{5}{7}+\dfrac{1}{2}-\dfrac{12}{17}-\dfrac{1}{2}+\dfrac{5}{9}=\left(\dfrac{1}{9}+\dfrac{5}{9}\right)+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)-\dfrac{5}{7}-\dfrac{12}{17}=\dfrac{2}{3}-\dfrac{5}{7}-\dfrac{12}{17}=\dfrac{238-255-252}{357}=\dfrac{-269}{357}.\)
H
2
13 tháng 11 2015
để 6*3 chia hết cho 9
=> 6+ * +3 chia hết cho 9
=>9 + * chia hết cho 9
=>* = 0;9
vậy số cần tìm là 603 hoặc 693
21 tháng 1 2022
a: AC=AB=4(cm)
b: Xét ΔABC cân tại A có \(\widehat{B}=60^0\)
nên ΔABC đều
c: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
RC
21 tháng 1 2022
a) Xét ΔABC cân tại A, có:
AB=AC
Mà AB=4 cm (gt)
⇒AC=4 cm
b)Xét ΔABC cân tại A, có:
Góc B=Góc C
Ta có : Góc A + Góc B + Góc C =180o (Tổng 3 góc trg 1Δ)
Mà Góc A= 60o(gt);Góc B=Góc C (cmt)
⇒Góc B= Góc C=60o
Xét ΔABC cân tại A, có:
Góc A= Góc B= Góc C(=60o)
⇒ΔABC đều
c)Xét ΔAMB và ΔAMC , có:
AB=AC (cmt)
BM=CM (M là tđ của BC)
AM là cạnh chung
⇒ΔAMB = ΔAMC (c.c.c)
20 tháng 9 2021
hơi giống ảnh mạng vì mình xem trên mạng và vẽ theo nhé bạn
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
Áp dụng định lý Pitago ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{9^2+12^2}\)
\(\Rightarrow BC=15\)
Ta có:
\(sinC=\dfrac{AB}{BC}=\dfrac{9}{15}\Rightarrow sinC=\dfrac{3}{5}\)
\(\Rightarrow C\approx36^052'\)
\(B=90^0-C=53^08'\)
23 tháng 7 2021
a) Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{9}{15}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)
Gải chi tiết hộ em ạ Cảm ơn !
6 tháng 1 2021
Xét phương trình đã cho. Ta có \(VT=\sqrt{3\left(x+1\right)^2+1}\ge1;VP=2-2x-x^2=1-\left(x+1\right)^2\le0\) nên \(VT\ge VP\).
Đẳng thức xảy ra khi và chỉ khi \(x+1=0\Leftrightarrow x=-1\).
Vậy nghiệm của phương trình là x = -1.
\(S=\dfrac{2}{1\cdot4}+\dfrac{2}{4\cdot7}+\dfrac{2}{7\cdot10}+\dfrac{2}{10\cdot13}+\dfrac{2}{13\cdot16}+\dfrac{2}{16\cdot19}+\dfrac{2}{19\cdot22}\)
\(S=\dfrac{2\cdot1}{1\cdot4}+\dfrac{2\cdot1}{4\cdot7}+\dfrac{2\cdot1}{7\cdot10}+\dfrac{2\cdot1}{10\cdot13}+\dfrac{2\cdot1}{13\cdot16}+\dfrac{2\cdot1}{16\cdot19}+\dfrac{2\cdot1}{19\cdot22}\)
\(S=2\cdot\left(\dfrac{1}{1\cdot4}+\dfrac{1}{4\cdot7}+\dfrac{1}{7\cdot10}+\dfrac{1}{10\cdot13}+\dfrac{1}{13\cdot16}+\dfrac{1}{16\cdot19}+\dfrac{1}{19\cdot22}\right)\)
\(S=2\cdot\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{22}\right)\)
\(S=2\cdot\left(1-\dfrac{1}{22}\right)\)
\(S=2\cdot\dfrac{21}{22}\)
\(S=\dfrac{42}{22}\)
\(S=\dfrac{21}{11}\)