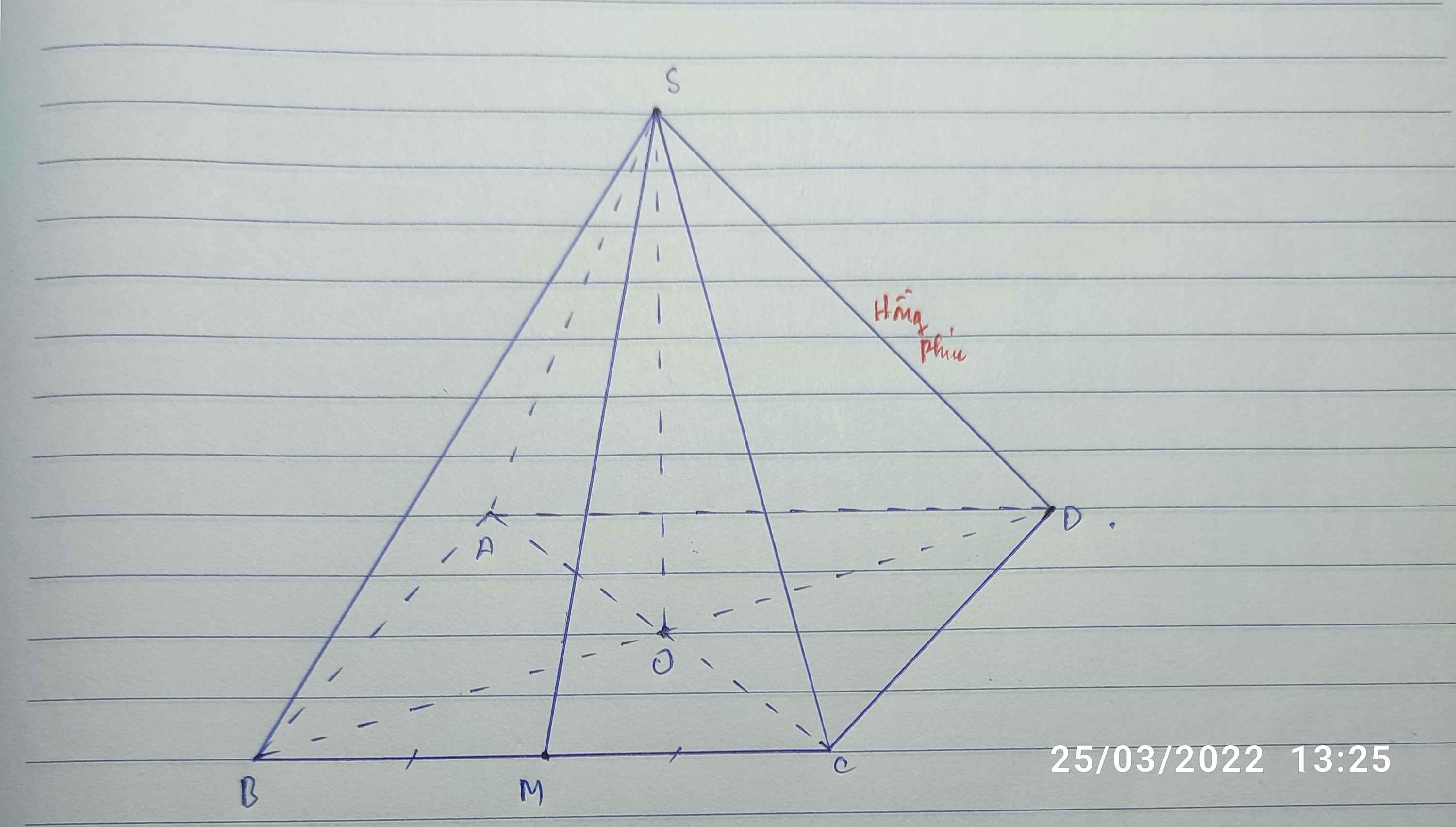
cho hình chóp S.ABCD có đáy là hình vuông , gọi O là tâm của đáy SO vuông góc (ABCD)
a)Chứng minh BD vuông góc với (SAC)
b) gọi M là trung điểm của BC .Chứng minh SM vuông góc AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HP
Hồng Phúc
25 tháng 3 2022
Đúng(0)
HP
Hồng Phúc
25 tháng 3 2022
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 3 2021
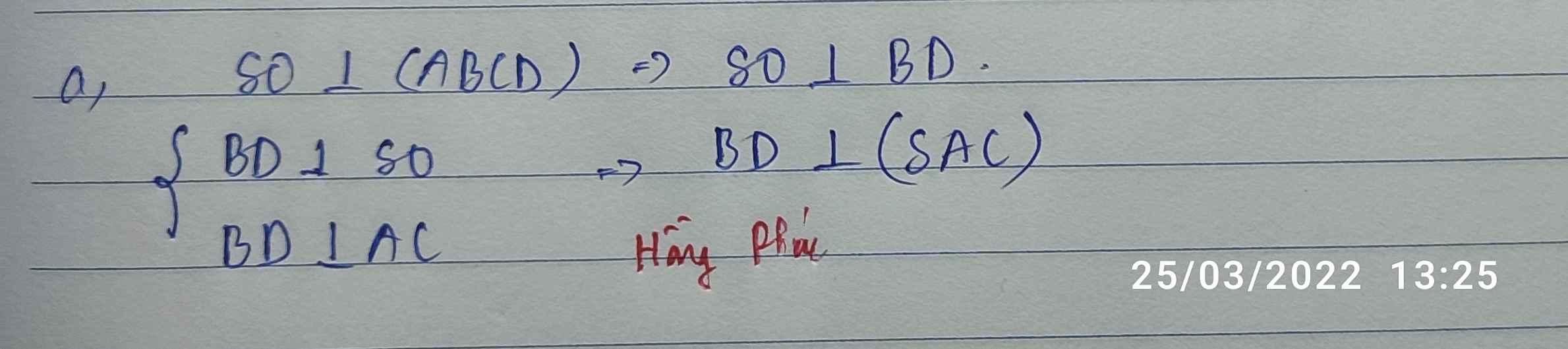
Gọi N là trung điểm AB \(\Rightarrow MN\perp AD\Rightarrow AD\perp\left(SMN\right)\Rightarrow AD\perp SM\)
Mặt khác: \(MN=AB=a\) ; \(SM=SN=\sqrt{SO^2+\left(\dfrac{MN}{2}\right)^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow SM^2+SN^2=MN^2\Rightarrow\Delta SMN\) vuông cân tại S hay \(SM\perp SN\)
\(\Rightarrow SM\perp\left(SAD\right)\)
Trong mp (SBC), dựng hình chữ nhật SMCP \(\Rightarrow CP||SM\Rightarrow CP\perp\left(SAD\right)\)
\(\Rightarrow\) SP là hình chiếu vuông góc của SC lên (SAD) hay \(\widehat{CSP}=\phi\)
\(AC=a\sqrt{5}\Rightarrow SC=\sqrt{SO^2+\left(\dfrac{AC}{2}\right)^2}=\dfrac{a\sqrt{6}}{2}\); \(SP=MC=\dfrac{BC}{2}=a\)
\(\Rightarrow CP=\sqrt{SC^2-SP^2}=\dfrac{a\sqrt{2}}{2}\)
\(sin\phi=\dfrac{CP}{SC}=\dfrac{\sqrt{3}}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
\(AC=\sqrt{AB^2+BC^2}=2a\) \(\Rightarrow AO=\dfrac{1}{2}AC=a\) ; \(AM=\dfrac{1}{2}AO=\dfrac{a}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD) \(\Rightarrow\widehat{SCA}=45^0\)
\(\Rightarrow SA=AC.tan45^0=2a\)
\(AB^2=a^2\) ; \(AM.AC=\dfrac{a}{2}.2a=a^2\Rightarrow AB^2=AM.AC\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AC}{AB}\Rightarrow\Delta ABM\sim\Delta ACB\left(c.g.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{ABC}=90^0\Rightarrow BM\perp AC\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BM\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\left(SBM\right)\perp\left(SAC\right)\)
6 tháng 7 2023
a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2021
Ta có: \(AC=\sqrt{AB^2+BC^2}=a\sqrt{3}\) ;
\(AM=\dfrac{AD}{2}=\dfrac{a\sqrt{2}}{2}\Rightarrow BM=\sqrt{AB^2+AM^2}=\dfrac{a\sqrt{6}}{2}\)
Áp dụng định lý talet:
\(\dfrac{AI}{IC}=\dfrac{MI}{BI}=\dfrac{AM}{BC}=\dfrac{1}{2}\Rightarrow\left\{{}\begin{matrix}IC=\dfrac{2}{3}AC=\dfrac{2a\sqrt{3}}{3}\\IB=\dfrac{2}{3}BM=\dfrac{a\sqrt{6}}{3}\end{matrix}\right.\)
\(\Rightarrow IB^2+IC^2=2a^2=BC^2\)
\(\Rightarrow\Delta IBC\) vuông tại I \(\Rightarrow BM\perp AC\Rightarrow BM\perp\left(SAC\right)\)
Mà \(BM\in\left(SMB\right)\Rightarrow\left(SAC\right)\perp\left(SMB\right)\)
22 tháng 4 2023
1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
BD vuông góc CA
BD vuông góc SA
=>BD vuông góc (SAC)
2: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SCD) vuông góc (SAD)
4: (SC;(SAB))=(SC;SB)=góc CSB
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{AC^2+SA^2}=a\sqrt{5}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
BC=a
Vì SB^2+BC^2=SC^2
nên ΔSCB vuông tại B
sin CSB=BC/SC=1/căn 5
=>góc CSB=27 độ
3: BC vuông góc SAB
=>AE vuông góc BC
mà AE vuông góc SB
nên AE vuông góc (SBC)
=>AE vuông góc SC
4: (SB;(SAC))=(SB;SD)=góc DSB
\(SD=\sqrt{SA^2+AD^2}=2a;SB=2a;DB=a\sqrt{2}\)
\(cosDSB=\dfrac{4a^2+4a^2-2a^2}{2\cdot2a\cdot2a}=\dfrac{3}{4}\)
=>góc DSB=41 độ
22 tháng 4 2023
1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
BD vuông góc CA
BD vuông góc SA
=>BD vuông góc (SAC)
2: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
=>(SCD) vuông góc (SAD)
4: (SC;(SAB))=(SC;SB)=góc CSB
\(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(SC=\sqrt{AC^2+SA^2}=a\sqrt{5}\)
\(SB=\sqrt{SA^2+AB^2}=2a\)
BC=a
Vì SB^2+BC^2=SC^2
nên ΔSCB vuông tại B
sin CSB=BC/SC=1/căn 5
=>góc CSB=27 độ
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
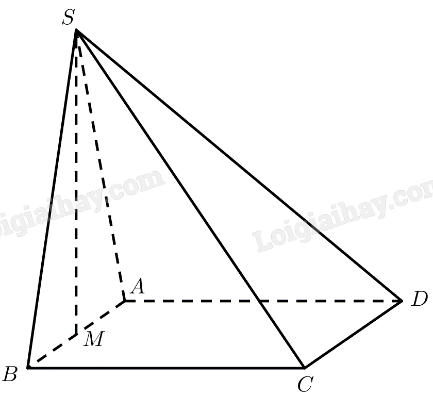
a, Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
30 tháng 4 2022
Có : AC vuông góc với BD (hình vuông ABCD)
SA vuông góc với BD ( do SA vuông góc với mp ABCD)
=> BD vuông góc với mp SAC...