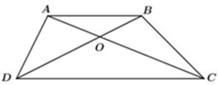
Câu 1: Cho ΔABC có AC>BC>AB. Trong các khẳng định sau, câu nào đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


có A C > B C > A B nên theo quan hệ giữa cạnh và góc trong tam giác ta có: C ^ < A ^ < B ^
Đáp án C

Do ∠A là góc tù nên ∠A lớn nhất. Vậy có ∠A> ∠B > ∠C. Từ đó suy ra BC > AC > AB. Chọn (D) BC > AC > AB.

Lời giải:
Theo tính chất góc đối diện với cạnh lớn hơn thì lớn hơn, từ $AC< BC< AB$ suy ra $\widehat{B}< \widehat{A}< \widehat{C}$
Đáp án C>

Vì AB // CD, áp dụng định lý Talet, ta có: O A O C = A B C D = O B O D
=> O A O C = A B C D ó OA.OD = OB.OC
=> Khẳng định (I) O A O C = A B C D đúng, khẳng định (II) O B O C = B C A D sai, khẳng định (III) OA.OD = OB.OC đúng
Vậy có 2 khẳng định đúng.
Đáp án: B

Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{5}{7}\)
=>\(\dfrac{BD}{5}=\dfrac{DC}{7}\)
mà BD+DC=BC=6
nên \(\dfrac{BD}{5}=\dfrac{CD}{7}=\dfrac{BD+CD}{5+7}=\dfrac{6}{12}=\dfrac{1}{2}\)
=>BD=2,5; CD=3,5
=>\(\dfrac{BD}{BC}=\dfrac{5}{12};\dfrac{CD}{CB}=\dfrac{7}{12}\)
\(\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}\)
\(=\overrightarrow{AB}+\dfrac{5}{12}\cdot\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{5}{12}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{7}{12}\cdot\overrightarrow{AB}+\dfrac{5}{12}\cdot\overrightarrow{AC}\)
=>Chọn C

Xét hai tam giác vuông ABC và DFE có: ∠A = ∠D = 90º ; AC=DE
a) Thêm điều kiện BC=EF thì ΔABC=ΔDFE (cạnh huyền - cạnh góc vuông).
b) Thêm điều kiện ∠C = ∠E thì ΔABC=ΔDFE (g.c.g).
c) Thêm điều kiện ∠C = ∠F thì ta không thể kết luận ΔABC=ΔDFE
a) Đúng;
b) Đúng;
c) Sai.
C
C