Cho (P) y=x2 và đường thẳng (d): y=(m2-4)x+m2-3 (m là tham số).
a) Tìm tọa độ giao điểm của (P) với đường thẳng (d) khi m=0
b) Tìm các giá trị của tham số m để đường thẳng d luôn cắt (P) tại hai điểm phân biệt
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 6 2023
a: Thay x=0 và y=-5 vào (d), ta được:
2(m+1)*0-m^2-4=-5
=>m^2+4=5
=>m=1 hoặc m=-1
b:
PTHĐGĐ là;
x^2-2(m+1)x+m^2+4=0
Δ=(2m+2)^2-4(m^2+4)
=4m^2+8m+4-4m^2-16=8m-12
Để PT có hai nghiệm phân biệt thì 8m-12>0
=>m>3/2
x1+x2=2m+2; x1x2=m^2+4
(2x1-1)(x2^2-2m*x2+m^2+3)=21
=>(2x1-1)[x2^2-x2(2m+2-2)+m^2+4-1]=21
=>(2x1-1)[x2^2+2x2-x2(x1+x2)+x1x2-1]=21
=>(2x1-1)(x2^2+2x2-x1x2-x2^2+x1x2-1]=21
=>(2x1-1)(2x2-1)=21
=>4x1x2-2(x1+x2)+1=21
=>4(m^2+4)-2(2m+2)+1=21
=>4m^2+16-4m-4-20=0
=>4m^2-4m-8=0
=>(m-2)(m+1)=0
=>m=2(nhận) hoặc m=-1(loại)
25 tháng 5 2022
b: Khi m=2 thì \(y=\left(2\cdot2-1\right)x-2^2+2=3x-2\)
Phương trình hoành độ giao điểm là:
\(x^2-3x+2=0\)
=>x=2 hoặc x=1
Khi x=2 thì y=4
Khi x=1 thì y=1
c: Phương trình hoành độ giao điểm là:
\(x^2-\left(2m-1\right)x+m^2-2=0\)
\(\text{Δ}=\left(2m-1\right)^2-4\left(m^2-2\right)\)
\(=4m^2-4m+1-4m^2+8=-4m+9\)
Để (P) cắt (d) tại hai điểm phân biệt thì -4m+9>0
=>-4m>-9
hay m<9/4
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2021
b. Phương trình hoành độ giao điểm:
\(x^2=4x-m\Leftrightarrow x^2-4x+m=0\) (1)
d cắt (P) tại 2 điểm phân biệt khi và chỉ khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta'=4-m>0\Rightarrow m< 4\)
Khi đó kết hợp hệ thức Viet và điều kiện đề bài:
\(\left\{{}\begin{matrix}x_1+x_2=4\\2x_1+x_2=-5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=4\\x_1=-9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-9\\x_2=13\end{matrix}\right.\)
Mà \(x_1x_2=m\)
\(\Rightarrow m=-9.13=-117\)
2 tháng 4 2021
a) Thay m=6 vào (d), ta được: y=4x-6
Phương trình hoành độ giao điểm của (P) và (d) là:
\(2x^2=4x-6\)
\(\Leftrightarrow2x^2-4x+6=0\)
\(\text{Δ}=\left(-4\right)^2-4\cdot2\cdot6=16-48=-32\)(loại)
Vì Δ<0 nên phương trình vô nghiệm
Vậy: Khi m=6 thì (P) và (d) không có điểm chung
AT
13 tháng 6 2021
a) pt hoành độ giao điểm: \(x^2-2x+3-m^2=0\)
Để đường thẳng d cắt (P) tại 2 điểm phân biệt thì \(\Delta'>0\)
\(\Delta'=1+m^2-3\Rightarrow m^2-2>0\Rightarrow\left|m\right|>\sqrt{2}\)
b) Gọi giao điểm là \(A\left(x_1,y_1\right);B\left(x_2,y_2\right)\)
\(\Rightarrow A\left(x_1,x_1^2\right);B\left(x_2,x_2^2\right)\)
Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=3-m^2\end{matrix}\right.\)
Theo đề: \(y_1-y_2=8\Rightarrow x_1^2-x_2^2=8\Rightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)=8\)
\(\Rightarrow x_1-x_2=4>0\)
Ta có: \(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=4m^2-8\)
\(\Rightarrow x_1-x_2=\sqrt{4m^2-8}\left(x_1-x_2>0\right)\Rightarrow4=\sqrt{4m^2-8}\)
\(\Rightarrow4m^2-8=16\Rightarrow m=\pm\sqrt{6}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
18 tháng 5 2021
1/
\(\hept{\begin{cases}3x+4y=6\left(1\right)\\2x-y=-7\left(2\right)\end{cases}}\)
\(\left(2\right)\Leftrightarrow8x-4y=-28\left(3\right)\)
Cộng 2 vế của (1) với (3) \(\Rightarrow11x=-22\Rightarrow x=-2\) Thay vào (2) \(\Rightarrow2.\left(-2\right)-y=-7\Rightarrow y=3\)
2/
a/ d cắt p tại 2 điểm phân biệt khi \(x^2=5x+m\Leftrightarrow x^2-5x-m=0\) có 2 nghiệm phân biệt
Điều kiện \(\Delta=25+4m>0\Leftrightarrow m>-\frac{25}{4}\)
b/ Khi m=-4
\(x^2-5x+4=0\Rightarrow x_1=1;x_2=4\)
Khi m=-4 d cắt p tại 2 điểm phân biệt A(1;0) và B(4;0)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Phương trình hoành độ giao điểm:
\(-\dfrac{1}{2}x^2=mx+m-3\Leftrightarrow x^2+2mx+2m-6=0\) (1)
a. Khi \(m=-1\), (1) trở thành:
\(x^2-2x-8=0\Rightarrow\left[{}\begin{matrix}x=4\Rightarrow y=-8\\x=-2\Rightarrow y=-2\end{matrix}\right.\)
Vậy (d) cắt (P) tại 2 điểm có tọa độ là \(\left(4;-8\right)\) ; \(\left(-2;-2\right)\)
b.
\(\Delta'=m^2-2m+6=\left(m+1\right)^2+5>0;\forall m\Rightarrow\left(1\right)\) có 2 nghiệm pb với mọi m
Hay (d) cắt (P) tại 2 điểm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=14\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)
\(\Leftrightarrow4m^2-2\left(2m-6\right)=14\)
\(\Leftrightarrow4m^2-4m-2=0\Rightarrow m=\dfrac{1\pm\sqrt{3}}{2}\)
CM
25 tháng 9 2017
b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
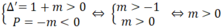
Khi đó 2 nghiệm của phương trình là:
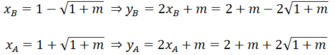
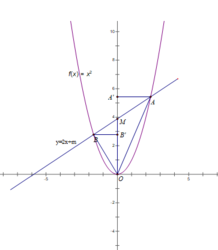
Kẻ BB' ⊥ OM ; AA' ⊥ OM
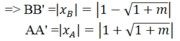
Ta có:
S A O M = 1/2 AA'.OM ; S B O M = 1/2 BB'.OM
Theo bài ra:
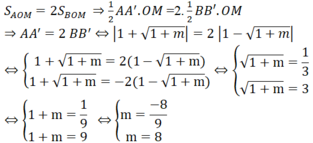
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.
15 tháng 5 2021
a) Xét phương trình hoành độ giao điểm chung của (d) và (P) :
\(x^2=\left(2m-1\right)x-m^2+2\)
\(\Leftrightarrow x^2-\left(2m-1\right)x+m^2-2=0\left(1\right)\)
Thay m=2 vào pt (1) ta được:
\(x^2-3x+2=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\Rightarrow y=1\\x=2\Rightarrow y=4\end{cases}}\)
Tọa độ giao điểm của (d) và (P) khi m=2 là \(A\left(1;1\right);B\left(2;4\right)\)
b) \(\Delta_{\left(1\right)}=\left(2m-1\right)^2-4m^2+8\)
\(=4m^2-4m+1-4m^2+8\)
\(=9-4m\)
Để pt (1) có 2 n ghiệm pb \(\Leftrightarrow9-4m>0\Leftrightarrow m< \frac{9}{4}\)
Theo hệ thức Vi-et ta có:
\(\hept{\begin{cases}x_1+x_2=2m-1\\x_1.x_2=m^2-2\left(1\right)\end{cases}}\)
Ta có: \(\hept{\begin{cases}x_1+x_2=2m-1\\x_1-3x_2=7\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3x_1+3x_2=6m-3\\x_1-3x_2=7\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1=\frac{3m+2}{2}\\x_2=\frac{m-4}{2}\end{cases}\left(3\right)}\)
Thay (3) vào (2) ta được:
\(\frac{3m+2}{2}.\frac{m-4}{2}=m^2-2\)
\(\Leftrightarrow\frac{3m^2-10m-8}{4}=m^2-2\)
\(\Rightarrow3m^2-10m-8=4m^2-8\)
\(\Leftrightarrow m^2+10m=0\)
\(\Leftrightarrow\orbr{\begin{cases}m=0\\m=-10\end{cases}\left(tm\right)}\)
Vậy ...
a, Thay m = 0 ta được (d) : y = -4x - 3
Hoành độ giao điểm (P) ; (d) tm pt
\(x^2+4x+3=0\Leftrightarrow x=-1;x=-3\)
Với x = -1 => y = 1
Với x = -3 => y = 9
Vậy (P) cắt (d) tại A(-1;1) ; B(-3;9)
b, Hoành độ giao điểm (P) ; (d) tm pt
\(x^2-\left(m^2-4\right)x-m^2+3=0\)
\(\Delta=\left(m^2-4\right)^2-4\left(-m^2+3\right)\)
\(=m^4-8m^2+16+4m^2-12=m^4-4m^2+4=\left(m^2-2\right)^2\)
Để pt luôn có 2 nghiệm pb khi \(m^2-2\ne0\Leftrightarrow m\ne\pm\sqrt{2}\)
a.
*)với m =0 thì (d): y=-4x-3
*) Xét....: x2=-4x-3 ⇔ x2+4x+3=0
Vì 1-4+3=0 nên PT có nghiệm x1=-1 hoặc x2=-3
* )x1=-1 thì y1=1 =>A(...)
*)x2=-3 thì y2=9 => B(..)
b) Xét ...............
x2=(m2-4)x+m2-3
⇔x2-(m2-4)x-m2+3=0 (1)
a=1; b=-(m2-4); c=-m2+3
Để.......... (1) có 2 nghiệm phân biệt
Cách 1: Δ>0 (Tự làm)
Cách 2: a-b+c=1+(m2-4)-m2+3=0
Pt(1) có 2 nghiệm:
x1=-1 và x2=-(-m2+3)=m2-3
Để.... thì x1≠x2 hay: m2-3≠-1 ⇒m≠\(\pm\sqrt{2}\)
Vậy với m≠\(\pm\sqrt{2}\) thì đường thẳng d luôn cắt (P) tại hai điểm phân biệt.