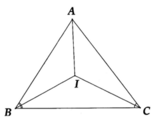
Cho tam giác ABC có I là giao điểm của 2 tia phân giác góc B và C .Biết BIC =140 độ.Tính góc A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
17 tháng 2 2021
Lời giải:Áp dụng định lý tổng 3 góc trong tam giác đối với tam giác $BIC$ và $ABC$:
$\widehat{BIC}=180^0-(\widehat{IBC}+\widehat{ICB})$
$=180^0-(\frac{\widehat{B}}{2}+\frac{\widehat{C}}{2})$
$=180^0-\frac{\widehat{B}+\widehat{C}}{2}=180^0-\frac{180^0-\widehat{A}}{2}$
$=180^0-\frac{180^0-60^0}{2}=120^0$
23 tháng 7 2018
+) Trong tam giác ABC có: ^BAC = a => ^ABC + ^ACB = 1800 - a <=> (^ABC + ^ACB)/2 = 900 - a/2
=> ^IBC + ^ICB = 900 - a/2 => ^BIC = 1800 - 900 + a/2 = 900 +a/2
+) ^BIC = 2.^BAC = 2a => a = (900 + a/2) / 2 = 450 + a/4 <=> 3/4.a = 450 <=> a= 450 . 4/3 = 600
Vậy nếu ^BIC = 2.^BAC thì ^BAC = a = 600.
8 tháng 1 2021
a) Vì BI là tia phân giác của \(\widehat{ABC}\)
nên \(\widehat{IBC}=\dfrac{\widehat{ABC}}{2}\)
Vì CI là tia phân giác của \(\widehat{ACB}\)
nên \(\widehat{ICB}=\dfrac{\widehat{ACB}}{2}\)
Xét ΔABC có
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=180^0-\widehat{A}\)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=180^0-80^0=100^0\)
Ta có: \(\widehat{IBC}+\widehat{ICB}=\dfrac{\widehat{ABC}}{2}+\dfrac{\widehat{ACB}}{2}\)
\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=\dfrac{\widehat{ABC}+\widehat{ACB}}{2}=\dfrac{100^0}{2}\)
hay \(\widehat{IBC}+\widehat{ICB}=50^0\)
Xét ΔBIC có
\(\widehat{BIC}+\widehat{IBC}+\widehat{ICB}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{BIC}+50^0=180^0\)
\(\Leftrightarrow\widehat{BIC}=180^0-50^0\)
hay \(\widehat{BIC}=130^0\)
Vậy: \(\widehat{BIC}=130^0\)
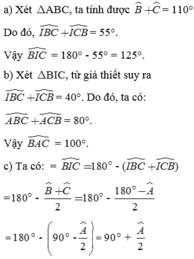
A=40 độ
Bạn có thể chỉ giúp mik cách giải được không Lê Bá Ngọc. Thanks bạn nhìu