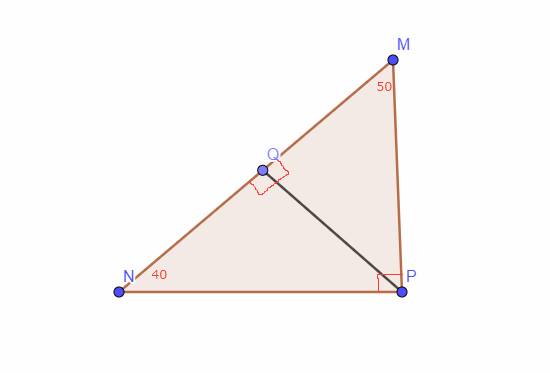
Cho hình vẽ biết góc MNP + NPQ bằng 180 độ góc MPQ bằng 50 độ Qx
vuông góc với PQ. Tính góc NMP và góc NRx
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
IM
1 tháng 10 2016
Dễ thấy MR // PQ
\(\Rightarrow\widehat{RMP}+\widehat{MPQ}=180^0\)
\(\Rightarrow\widehat{RMP}+50^0=180^0\)
\(\Rightarrow\widehat{RMP}=30^0\)
DD
1
12 tháng 1 2023
Xét Tam giác `MPQ` có:
\(\widehat{M}+\widehat{MPQ}+\widehat{MQP}=180^0\) (đli tổng 2 góc trong 1 Tam giác)
\(50^0+\widehat{MPQ}+90^0=180^0\)
`=>` \(\widehat{MPQ}=40^0\)
\(\widehat{MQP}+\widehat{NQP}=180^0\) (kề bù)
\(90^0+\widehat{NQP}=180^0\)
`=>` \(\widehat{NQP}=90^0\)
Xét Tam giác `NPQ` có:
\(\widehat{N}+\widehat{NQP}+\widehat{NPQ}=180^0\)
\(40^0+90^0+\widehat{NPQ}=180^0\)
`=>` \(\widehat{NPQ}=50^0\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) \(PQ = n.\cos a,PQ = m.\cos b\)
b) \(MQ = n.\sin a,PN = m.\sin b \Rightarrow MN = n.\sin a + m.\sin b\)
\(\begin{array}{l}{S_{MPQ}} = \frac{1}{2}m.\cos b.n.\sin a = \frac{1}{2}m.n.\cos b.\sin a\\{S_{NPQ}} = \frac{1}{2}n.\cos a.m.\sin b = \frac{1}{2}m.n.\cos a.\sin b\\{S_{MNP}} = \frac{1}{2}m.n.\sin \left( {a + b} \right)\end{array}\)
c) \({S_{MNP}} = {S_{MPQ}} + {S_{NPQ}} \Rightarrow \frac{1}{2}m.n.\cos b.\sin a + \frac{1}{2}m.n.\cos a.\sin b = \frac{1}{2}m.n.\sin \left( {a + b} \right)\)
\( \Rightarrow \sin \left( {a + b} \right) = \sin a.\cos b + \cos a.\sin b\)
d) \(\sin \left( {a - b} \right) = \sin \left[ {a + \left( { - b} \right)} \right] = \sin a.\cos \left( { - b} \right) + \cos a.\sin \left( { - b} \right) = \sin a.\cos b - \cos a.\sin b\)
