Cho hình chữ nhật $A B C D$ biết $A D=1$. Giả sử $\mathrm{E}$ là trung điểm $\mathrm{AB}$ và thỏa mãn $\sin \widehat{B D E}=\dfrac{1}{3}$.
Tính độ dài cạnh $A B$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 9 2018
Chọn C.
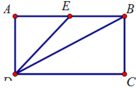
Đặt AB = 2x suy ra AE = EB = x.
Vì góc BDE nhọn nên 
suy ra
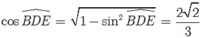
Theo định lí Pitago ta có:
DE2 = AD2 + AE2 = 1 + x2 nên 
BD2 = DC2 + BC2 = 4x2 + 1 nên 
Áp dụng định lí côsin trong tam giác BDE ta có
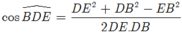
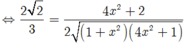
Suy ra: 4x4 - 4x2 + 1 = 0 nên 
(do x > 0)
Vậy độ dài cạnh AB là 
.
28 tháng 4 2021
Lời giải chi tiết
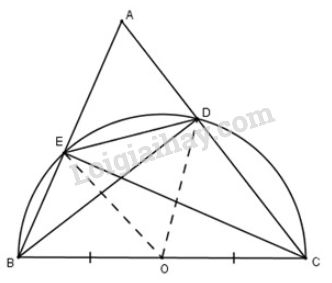
a) Gọi OO là trung điểm của BC⇒OB=OC=BC2.BC⇒OB=OC=BC2. (1)
Vì DODO là đường trung tuyến của tam giác vuông DBCDBC.
Theo tính chất trung tuyến ứng với cạnh huyền, ta có:
OD=12BCOD=12BC (2)
Từ (1) và (2) suy ra OD=OB=OC=12BCOD=OB=OC=12BC
Do đó ba điểm B, D, CB, D, C cùng thuộc đường tròn tâm OO bán kính OBOB.
Lập luận tương tự, tam giác BEC vuông tại E có EO là đường trung tuyến ứng với cạnh huyền BC nên OE=OB=OC=12BCOE=OB=OC=12BC
Suy ra ba điểm B, E, CB, E, C cùng thuộc đường tròn tâm OO bán kính OBOB.
Do đó 4 điểm B, C, D, EB, C, D, E cùng thuộc đường tròn (O)(O) đường kính BCBC.
b) Xét đường (O;BC2)(O;BC2), với BCBC là đường kính.
Ta có DEDE là một dây cung không đi qua tâm nên ta có BC>DEBC>DE ( vì trong một đường tròn, dây lớn nhất là đường kính).
PT
13 tháng 5 2021
a. Xét (O) , có:
CD \(\perp\)AB = {H}
=> \(\widehat{CHA}=90^o\Rightarrow\widehat{CHE}=90^o\)
Có: \(\widehat{CMD}\)là góc nội tiếp chắn nửa đường tròn đường kính CD
=> \(\widehat{CMD}=90^o\Rightarrow\widehat{CME}=90^o\)
Xét tứ giác CMEH, có:
\(\widehat{CME}+\widehat{CHE}=90^o+90^o=180^o\)
2 góc \(\widehat{CME}\)và \(\widehat{CHE}\)là 2 góc đối nhau
=> CMEH là tứ giác nội tiếp (đpcm)
15 tháng 5 2021
Câu a: Có góc CHE=90 độ (vì CD\(\perp AB\) tại H)
Góc CMD =90 độ(góc nt chắn nửa đt)
Mà góc CHE và góc CMD ở vị trí đối nhau
⇒ Tứ giác CMEH nội tiếp
Câu b:
Xét \(\Delta NACva\Delta NMB\) có :
Góc N chung
Góc NCA = góc NBM (cùng chắn cung MA)
⇒ \(\Delta NAC\) đồng dạng \(\Delta NBM\) (góc góc)
⇒\(\dfrac{NM}{NA}\)=\(\dfrac{NB}{NC}\)⇔NM.NC=NA.NB
Câu c:
Có góc PMA=90 độ ( góc nt chắn nửa đt)→PM\(\perp\)AK
Mà IK\(\perp\)AK
⇒IK song song với MP (từ vuông góc đến song song