Cho tam giác ABC, đường phân giác AD. Chứng minh AD2 = AB.AC - DB.DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 4 2019
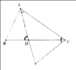
a) HS tự chứng minh.
b) HS tự chứng minh.
c) Từ a, suy ra AB.AC = AD.AI (1)
Từ b, suy ra BD.CD = AD.ID (2)
Từ (1) và (2), ta chứng minh được AD2 = AB.AC- DB.DC
SN
2
29 tháng 5 2021
Trên cùng một nửa mặt phẳng bờ \(BC\)không chứa \(A\)lấy tia \(Cx\)sao cho \(\widehat{BAD}=\widehat{BCx}\).
Kéo dài \(AD\)cắt \(Cx\)tại \(E\).
Xét \(\Delta DAB\)và \(\Delta DCE\)có:
\(\widehat{ADB}=\widehat{CDE}\)(vì đối đỉnh).
\(\widehat{BAD}=\widehat{BCE}\)(hình vẽ trên).
\(\Rightarrow\Delta DAB~\Delta DCE\left(g.g\right)\).
\(\Rightarrow\widehat{ABD}=\widehat{CED}\)(2 góc tương ứng).
\(\Rightarrow\widehat{ABD}=\widehat{CEA}\)
Và \(\frac{AD}{CD}=\frac{DB}{DE}\)(tỉ số đồng dạng).
\(\Rightarrow AD.DE=BD.CD\)\(\left(1\right)\).
Xét \(\Delta BAD\)và \(\Delta EAC\)có:
\(\widehat{BAD}=\widehat{EAC}\)(giả thiết).
\(\widehat{ABD}=\widehat{AEC}\)(chứng minh trên).
\(\Rightarrow\Delta BAD~\Delta EAC\left(g.g\right)\).
\(\Rightarrow\frac{AD}{AC}=\frac{AB}{AE}\)(tỉ số đồng dạng).
\(\Rightarrow AD.AE=AB.AC\)\(\left(2\right)\).
Từ \(\left(1\right)\)và \(\left(2\right)\).
\(\Rightarrow AD.AE-AD.DE=AB.AC-BD.CD\).
\(\Rightarrow AD\left(AE-DE\right)=AB.AC-BD.CD\).
\(\Rightarrow AD.AD=AB.AC-BD.CD\).
\(\Rightarrow AD^2=AB.AC-BD.CD\)(điều phải chứng minh).
HG
2
27 tháng 3 2016
Trên tia AD lấy điểm E sao cho ^BEA = ^BCA.
Khi đó ^BED = ^ACD và ^BDE = ^ADC nên hai tam giác BDE và ADC đồng dạng
suy ra BD/AD = DE/DC
suy ra AD.DE = DB.DC (1).
Gọi F là điểm đối xứng với C qua đường thẳng AD
vì AD là phân giác ^BAC nên F thuộc AB,
từ tính chất đối xứng suy ra ^DFA = ^DCA và AF = AC,
vì ^DCA = ^BCA = ^BEA nên ^DFA = ^BEA,
cùng với ^A chung nên hai tam giác DFA và BEA đồng dạng,
suy ra AD/AB = AF/AE = AC/AE, suy ra AD.AE = AB.AC (2).
Từ (2) và (1) theo vế thì có AD.(AE - DE) = AB.AC - DB.DC, suy ra AD^2 = AB.AC - DB.DC.
16 tháng 4 2018
cho hỏi bài này và chứng minh theo tính chất của BĐT
cho tam giác ABC CD là giân giác của tam giác cm: CD^2
28 tháng 3 2021
b) Xét ΔADB và ΔCDE có
\(\widehat{ADB}=\widehat{CDE}\)(hai góc đối đỉnh)
\(\widehat{BAD}=\widehat{ECD}\)(gt)
Do đó: ΔADB\(\sim\)ΔCDE(g-g)
9 tháng 5 2023
a: Xét ΔABE và ΔADC có
góc ABE=góc ADC
góc BAE=góc DAC
=>ΔABE đồng dạng với ΔADC
b: Xét ΔDAC và ΔDBE có
góc DAC=góc DBE
góc ADC=góc BDE
=>ΔDAC đồng dạng với ΔDBE
=>DA/DB=DC/DE
=>DA*DE=DB*DC
17 tháng 7 2021
a) DB?, DC?
Ta có:\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)(tính chất đường phân giác)
⇒\(\dfrac{DB}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
Mặt khác \(\dfrac{DB}{3}=\dfrac{DC}{5}\)
\(\dfrac{DB}{3}=\dfrac{DC}{5}=\dfrac{DB+DC}{3+5}=\dfrac{BC}{8}=\dfrac{12}{8}=\dfrac{3}{2}\)
\(\dfrac{DB}{3}=\dfrac{3}{2}\\ \Rightarrow DB=\dfrac{3\times3}{2}=\dfrac{9}{2}=4.5\left(cm\right)\)
Và \(\dfrac{DC}{5}=\dfrac{3}{2}\\ \Rightarrow DC=\dfrac{3\times5}{2}=\dfrac{15}{2}=7,5\left(cm\right)\)
Vậy DB=4,5(cm), DC= 7,5 cm
Bạn tự vẽ hình nhé :))
Từ B kẻ tia Bx cắt AD tại E sao cho góc ABE = góc ADC.
\(\Delta AEB\)và \(\Delta ACD\)có: góc ABE = góc ADC (cách dựng) và góc BAE = góc DAC (gt)
\(\Rightarrow\)\(\Delta AEB\)đồng dạng \(\Delta ACD\)\(\Rightarrow\)\(\frac{AB}{AD}=\frac{AE}{AC}\)\(\Rightarrow\)\(AB.AC=AE.AD\)(1)
\(\Rightarrow\)góc BED = góc ACD.
\(\Delta ACD\)và \(\Delta BED\)có: góc ACD = góc BED (cmt) và góc ADC = góc BDE (đối đỉnh)
\(\Rightarrow\)\(\Delta ACD\)đồng dạng \(\Delta BED\)\(\Rightarrow\)\(\frac{DB}{AD}=\frac{DE}{DC}\)\(\Rightarrow\)\(DB.DC=DE.AD\)(2)
Lấy (1) - (2) vế theo vế ta được \(AB.AC-DB.DC=AD\left(AE-DE\right)\)\(\Leftrightarrow\)\(AD^2=AB.AC-DB.DC\)(đpcm).
Cảm ơn bạn nhiều