Chứng minh 82 + 220 chia hết cho 17
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 12 2023
\(8^8+2^{20}\)
\(=\left(2^3\right)^8+2^{20}\)
\(=2^{24}+2^{20}\)
\(=2^{20}\left(2^4+1\right)\)
\(=2^{20}\cdot17⋮17\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 9 2023
Bài 1
a, cm : A = 165 + 215 ⋮ 3
A = 165 + 215
A = (24)5 + 215
A = 220 + 215
A = 215.(25 + 1)
A = 215. 33 ⋮ 3 (đpcm)
b,cm : B = 88 + 220 ⋮ 17
B = (23)8 + 220
B = 216 + 220
B = 216.(1 + 24)
B = 216. 17 ⋮ 17 (đpcm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 9 2023
c, cm: C = 1 - 2 + 22 - 23 + 24 - 25 + 26 -...-22021 + 22022 : 6 dư 1
C=1+(-2+22-23+24- 25+26)+...+(-22017+22018-22019+22020-22021+22022)
C = 1 + 42 +...+ 22016.(-2 + 22 - 23 + 24 - 25 + 26)
C = 1 + 42+...+ 22016.42
C = 1 + 42.(20+...+22016)
42 ⋮ 6 ⇒ C = 1 + 42.(20+...+22016) : 6 dư 1 đpcm
D
21 tháng 6 2017
a) Ta có:
\(7^{2006}-7^{2005}+7^{2004}\)
\(=7^{2004}\left(7^2-7+1\right)\)
\(=7^{2004}\times43\)
\(\Rightarrow7^{2006}-7^{2005}+7^{2004}\)chia hết cho 43 (vì có chứa thừa số 43)
b) Ta có:
\(32^{17}+16^{21}-2^{82}\)
\(=\left(2^5\right)^{17}+\left(2^4\right)^{21}-2^{82}\)
\(=2^{85}+2^{84}-2^{82}\)
\(=2^{82}\left(2^3+2^2-1\right)=2^{82}\times11=2^{80}\times2^2\times11\)
\(=2^{80}\times44\)
\(\Rightarrow32^{17}+16^{21}-2^{82}\)chia hết cho 44 (vì có chứa thừa số 44)
KV
23 tháng 12 2023
A = 8⁸ + 2²⁰
= (2³)⁸ + 2²⁰
= 2²⁴ + 2²⁰
= 2²⁰.(2⁴ + 1)
= 2²⁰.17 ⋮ 17
Vậy A ⋮ 17
OY
21 tháng 8 2021
b) A=2+22+23+...+220
A=(2+22)+(23+24)+...+(219+220)
A=3.2+3.23+...+3.219
A=3.(2+23+25+...+219)
⇒A⋮3
phần c) làm tương tự
NG
1
H9
HT.Phong (9A5)
CTVHS
17 tháng 10 2023
a) \(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{19}+2^{20}\right)\)
\(A=2\cdot\left(1+3\right)+2^3\cdot\left(1+3\right)+...+2^{59}\cdot\left(1+3\right)\)
\(A=3\cdot\left(2+2^3+...+2^{59}\right)\)
Vậy A chia hết cho 3
________
\(A=2+2^2+2^3+...+2^{20}\)
\(A=\left(2+2^3\right)+\left(2^2+2^4\right)+...+\left(2^{58}+2^{60}\right)\)
\(A=2\cdot\left(1+4\right)+2^2\cdot\left(1+4\right)+...+2^{58}\cdot\left(1+4\right)\)
\(A=5\cdot\left(2+2^2+...+2^{58}\right)\)
Vậy A chia hết cho 5
CM
7 tháng 7 2019
a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:
10 tháng 10 2021
4₁ A= 2 +2²³ +2 ² + + 220
a₁ A = 2₁ [1 + 2 +2²¹ +. +2¹2):2 Vay A chia hết choi
b₁ A = 2 + 2² +2²+ + 220 (2 +2²) + (2 ² + 2 9) + . + (219+220)
= 2₁ (1 + 2) + 2² (2+1). .. +2 19 (2+1) + = 2₁3 + 2³.3 + ..+ 219.3.
= (2+2 ³+ + 219) 3:3 Vậy A chia hết cho 3 A = 2 + 2 ² + 2³ + 2ª +. 20 + 2.9+ +2
2+2 ³ + 2² +2²4 + + 218 + 720 +2²³ +2²+ +218 +220 2. (2 +2²) + 2² (1+2²) +.. + 218 ( 1 +2²) = 2 5 +2²5 + + 218 5. 12 +2° + 2 ... +218 ) 5 : 5.
vậy A chia hết cho 5
13 tháng 7 2016
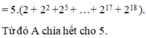
câu thứ 2
a - 5b chia hết cho 17 thì 10a-50b chia hết cho 17
10a-50b=10a+b-51b
51b chia hết cho 17 nên 10a+b chia hết cho 17
13 tháng 7 2016
51a : 17
=> 51a - a + 5b : 17
=> 50a + 5b : 17
=> 5 ( 10a + b ) : 17
=> 10a + b : 17
\(8^2+2^{20}=\left(2^3\right)^2+2^{20}=2^6+2^{20}=2^4.\left(2^2+2^{16}\right)=16.\left(2^2.2^{16}\right).\)
xin lỗi các bạn nha! mình viết nhầm đề
Chứng minh 88 + 220 chia hết cho 17