Cho tam giác DEF vuông tại F có DE=15cm EF=12cm. Tính DF Ét o ét cứu mìk vs mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
1
YP
22 tháng 3 2022
Xét tam giác DEF vuông tại F có:
\(DE^2=EF^2+DF^2\) (Định lý Pytago)
=> \(15^2=12^2+DF^2\)
=> 225 = 144 + \(DF^2\)
=> \(DF^2=\) 225-144 = 81
=> DF = \(\sqrt{81}\) = 9
23 tháng 4 2023
`@` `\text {dnammv}`
`a,`
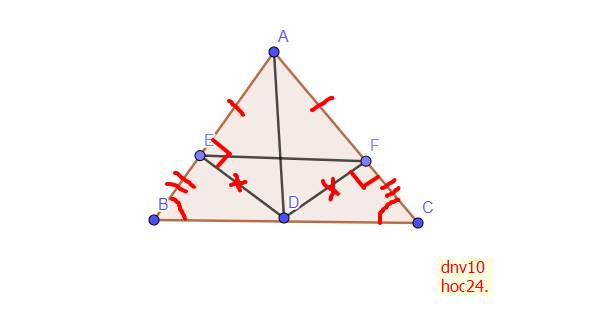
Xét \(\Delta BED\) và \(\Delta CFD\) có:
\(\left\{{}\begin{matrix}\text{BD = CD (D là trung điểm của BC}\\\widehat{\text{B}}=\widehat{\text{C}}\left(\text{ }\Delta\text{ABC cân tại A}\right)\\\widehat{BED}=\widehat{CFD}\left(=90^0\right)\end{matrix}\right.\)
`=> \Delta BED = \Delta CFD (ch-gn)`
`-> \text {BE = CF (2 cạnh tương ứng)}`
`b,`
Vì `\Delta BED = \Delta CFD (a)`
`-> \text {DE = DF (2 cạnh tương ứng)}`
`\text {Xét}` `\Delta DEF:`
`\text {DE = DF}`
`-> \Delta DEF` là `\Delta` cân
`c,`
Vì \(\left\{{}\begin{matrix}\text{AB = AC (tam giác ABC cân tại A)}\\\text{BE = CF (a)}\end{matrix}\right.\)
`-> \text {AE = AF}`
\(\text{Xét }\Delta\text{ AEF}: \)
`\text {AE = AF}`
`-> \Delta AEF` là `\Delta` cân (tại A).
`->`\(\widehat {AEF}= \widehat {AFE}\)\(=\dfrac{180-\widehat{A}}{2}\text{ }\left(1\right)\)
`\Delta ABC` cân tại `A`
`->`\(\widehat {ABC}= \widehat {ACB}=\)\(\dfrac{180-\widehat{A}}{2}\text{ }\left(2\right)\)
Từ `(1)` và `(2)`
`->`\(\widehat {AEF}= \widehat {ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {EF // BC (tính chất 2 đường thẳng //).}`
3 tháng 1 2022
Ta có: \(tanDFE=\dfrac{DE}{DF}=0,3\Rightarrow\widehat{DFE}\approx16^o42'\)
\(\Rightarrow DF=sinDFE.EF=sin16^o42'.15=4,31\left(cm\right)\)
16 tháng 3 2022
a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)
3 tháng 10 2021
\(a,\) Áp dụng Pytago \(EF=\sqrt{DE^2+DF^2}=25\left(cm\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}DE^2=EH\cdot EF\\DF^2=FH\cdot EF\\DH^2=FH\cdot EH\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}EH=\dfrac{DE^2}{EF}=9\left(cm\right)\\FH=\dfrac{DF^2}{EF}=16\left(cm\right)\\DH=\sqrt{9\cdot16}=12\left(cm\right)\end{matrix}\right.\)
\(b,\sin\widehat{E}=\cos\widehat{F}=\dfrac{DF}{EF}=\dfrac{4}{5}\approx\left\{{}\begin{matrix}\sin53^0\\\cos37^0\end{matrix}\right.\\ \Rightarrow\widehat{E}\approx53^0;\widehat{F}\approx37^0\)
19 tháng 6 2023
a: Trực tâm là điểm D
b: EF=căn 3^2+4^2=5cm
c: DF=căn 10^2-6^2=8cm
10 tháng 11 2023
a: ΔDEF vuông tại D
=>\(DE^2+DF^2=EF^2\)
=>\(EF^2=0,9^2+12^2=144,81\)
=>\(EF=\sqrt{144,81}\)(cm)
Xét ΔDEF vuông tại D có \(tanE=\dfrac{DF}{DE}\)
=>\(tanE=\dfrac{12}{0,9}=\dfrac{120}{9}=\dfrac{40}{3}\)
b: Xét ΔDEF vuông tại D có
\(sinF=\dfrac{DE}{EF}=\dfrac{0.9}{\sqrt{144,81}}\)
\(cosF=\dfrac{DF}{EF}=\dfrac{12}{\sqrt{144,81}}\)
\(tanF=\dfrac{0.9}{12}=\dfrac{9}{120}=\dfrac{3}{40}\)
\(cotF=\dfrac{12}{0.9}=\dfrac{40}{3}\)
14 tháng 2 2016
a) Dùng định lí py-ta-gô để chứng minh, ta thấy:
122 + 92 = 152
Vậy DEF là tam giác vuông. Tam giác này vuông tại E ( do DF là cạnh huyền )
b) Tia IE là tia đối của tia ED => 3 diểm I, E, D thẳng hàng và IE vuông góc với IF
Vậy cạnh cần tìm IF chính là cạnh huyền của tam giác vuông EFI.
Áp dụng định lí Pi-ta-gô, ta có:
IF2 = IE2 + EF2
IF2 = 52 + 122
IF2 = 25 + 144
IF2 = 169
IF = 13
Vậy độ dài IF là 13cm.
Áp dụng định lí Pytago ta có
\(DE^2=DF^2+FE^2\\ \Rightarrow DF=\sqrt{15^2-12^2}=9\)