Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Xét tam giác ABM và tam giác ACM ta có
AB = AC
AM _ chung
BM = CM
Vậy tam giác ABM = tam giác ACM (c.c.c)
b, đề sai rồi
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét ΔBHM vuông tại H và ΔCKM vuông tại K có
MB=MC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBHM=ΔCKM
Do AB=AC(gt)
=> Tg ABC cân tại A
Mà \(\widehat{A}=90^o\)
=> Tg ABC vuông cân tại A
#H
#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM` chung
`AB = AC (g``t)`
\(\widehat{AMB}=\widehat{AMC}=90^0\)
`=>` Tam giác `AMB =` Tam giác `AMC (ch-cgv)`
`b,` Vì Tam giác `AMB = ` Tam giác `AMC (a)`
`=>` \(\widehat{B}=\widehat{C}\) `(2` góc tương ứng `)`
`=>` \(\widehat{BAM}=\widehat{CAM}\) `( 2` góc tương ứng `)`
`=> AM` là tia phân giác của \(\widehat{BAC}\)
`c,` Xét Tam giác `AHM` và Tam giác `AKM` có:
`AM` chung
\(\widehat{HAM}=\widehat{KAM}(CMT)\)
`=>` Tam giác `AHM =` Tam giác `AKM (ch-gn)`
`=> AH = AK (2` cạnh tương ứng `)`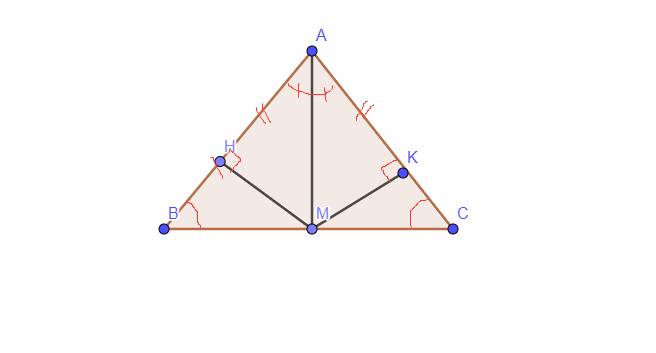
a) Xét tam giác ABE và tam giác ACF
Góc AEB = Góc AFC = 90 độ
Cạnh huyền AB=AC (theo giả thiết)
Góc A chung
Do đó: Tam giác ABE = Tam giác ACF (Cạnh huyền - góc nhọn )
Suy ra: AE=AF (2 cạnh tương ứng)
Xét tam giác AFH và tam giác AEH có:
Góc AFH= góc AEH = 90 độ
Cạnh huyền AH chung
AF=AE ( Chứng minh trên)
Do đó: tam giác AFH = tam giác AEH ( cạnh huyền cạnh góc vuông)
Suy ra góc FAH= góc EAH ( 2 góc tương ứng)
Hay GÓC BAH= GÓC CAH
Xét tam giác ABH và tam giác ACH có:
AB=AC( theo gt)
Góc BAH = Góc CAH ( chứng minh trên)
Cạnh AH chung
Do đó: tam giác ABH = tam giác ACH (c.g.c)
Vậy tam giác ABH = tam giác ACH (đpcm)
b) Vì tam giác ABC có AB=AC nên tam giác ABC là tam giác cân tại A, do đó suy ra góc B= góc C
Do Tam giác ABE = Tam giác ACF ( theo câu a ) nên suy ra BE=FC ( 2 cạnh tương ứng )
Ta có: AFC + CFB = 180 Độ (2 góc kề bù)
AEB + EBC = 180 độ ( 2 góc kề bù )
Mà AFC=AEB vì cùng bằng 90 độ nên CFB=BEC
Xét tam giác BFC và tam giác CEB có:
FB=EC ( chứng mình trên)
Góc B= góc C ( Theo trên)
Cạnh BC chung
Do đó tam giác BFC=tam giác CEB ( cạnh góc cạnh)
Vậy tam giác EBC= tam giác FCB (đpcm)
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=5^2-3^2=16\)
hay AC=4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{3^2}{5}=1.8\left(cm\right)\\CH=\dfrac{4^2}{5}=3.2\left(cm\right)\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot5=3\cdot4=12\)
hay AH=2,4cm
Bài 2:
Ta có: BC=HB+HC
nên BC=3,6+6,4
hay BC=10cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=3.6\cdot10=36\\AC^2=6.4\cdot10=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=6\left(cm\right)\\AC=8\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AH^2=6^2-3.6^2=23.04\)
hay AH=4,8cm
a: XétΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< Â\)
b: \(\widehat{C}=180^0-100^0-30^0=50^0\)
Xét ΔABC có \(\widehat{B}< \widehat{C}< \widehat{A}\)
nên AC<AB<BC
Câu hỏi là j vậy bạn?
Câu 3 : Cho tam giác ABC có Â = 900 và AB = AC ta có:
A. tam giác vuông ABC là tam giác vuông.
B. tam giác vuông ABC là tam giác cân.