21 x 22 x 23 x ... x 2x = 1024
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 12 2021
Sửa: \(A=1+2^1+2^2+2^3+...+2^{2021}\)
\(\Rightarrow A+1=1+1+2+2^2+...+2^{2021}\\ \Rightarrow A+1=2+2+2^2+...+2^{2021}\\ \Rightarrow A+1=2^2+2^2+2^3+...+2^{2021}\\ \Rightarrow A+1=2^3+2^3+2^4+...+2^{2021}\\ ....\\ \Rightarrow A+1=2^{2021}+2^{2021}=2^{2022}\)
Mà \(2^x=A+1\Rightarrow2^x=2^{2022}\Rightarrow x=2022\)
23 tháng 12 2021
\(A=1+2^1+2^1+2^2+...+2^{2021}\\ \Rightarrow A=1+2+2+2^2+...+2^{2021}\\ \Rightarrow A=1+2.2+2^2+...+2^{2021}\\ \Rightarrow A=1+2^2+2^2+...+2^{2021}\\ \Rightarrow A=1+2.2^2+...+2^{2021}\\ \Rightarrow A=1+2^3+...+2^{2021}\)
....
\(\Rightarrow A=1+2^{2022}\)
\(2^x=1+A\\ \Rightarrow2^x=1+1+2^{2022}\\ \Rightarrow2^x=2+2^{2022}\)
không phù hợp với lớp 6
CM
17 tháng 5 2017
a) 22 + (2x -13) = 83 => 2x -13 = 61 => x = 37.
b) 51 - (-12 + 3x) = 27 => 63 - 3x = 27 => x = 12.
c) - (2x + 2) + 21 = - 23 => 2x + 2 = 44 => x = 21.
d) 25 - (25 - x) = 0 => 25 - 25 + x = 0 => x = 0.
KV
23 tháng 10 2023
Bài 1
S₂ = 21 + 23 + 25 + ... + 1001
Số số hạng của S₂:
(1001 - 21) : 2 + 1 = 491
⇒ S₂ = (1001 + 21) . 491 : 2 = 250901
--------
S₄ = 15 + 25 + 35 + ... + 115
Số số hạng của S₄:
(115 - 15) : 10 + 1 = 11
⇒ S₄ = (115 + 15) . 11 : 2 = 715
KV
23 tháng 10 2023
Bài 2
a) 2x - 138 = 2³.3²
2x - 138 = 8.9
2x - 138 = 72
2x = 72 + 138
2x = 210
x = 210 : 2
x = 105
b) 5.(x + 35) = 515
x + 35 = 515 : 5
x + 35 = 103
x = 103 - 35
x = 78
c) 814 - (x - 305) = 712
x - 305 = 814 - 712
x - 305 = 102
x = 102 + 305
x = 407
d) 20 - [7.(x - 3) + 4] = 2
7(x - 3) + 4 = 20 - 2
7(x - 3) + 4 = 18
7(x - 3) = 18 - 4
7(x - 3) = 14
x - 3 = 14 : 7
x - 3 = 2
x = 2 + 3
x = 5
e) 9ˣ⁻¹ = 9
x - 1 = 1
x = 1 + 1
x = 2
VN
Võ Ngọc Phương
VIP
16 tháng 8 2023
a) \(A=2+2^2+2^3+...+2^{2022}\)
\(2A=2.\left(2+2^2+2^3+...+2^{2022}\right)\)
\(2.A=2^2+2^3+2^4+...+2^{2023}\)
\(2A-A=\left(2^2+2^3+2^4+...+2^{2023}\right)-\left(2+2^2+2^3+...+2^{2022}\right)\)
\(A=2^{2023}-2\)
b) A + 2 = 2x
Hay \(\left(2^{2023}-2\right)+2=2^x\)
\(2^{2023}-2+2=2^x\)
\(2^{2023}=2^x\)
\(\Rightarrow x=2023\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
a, A = 21 + 22 + 23 + ...+ 22022
2A = 22 + 23 +...+ 22022 + 22023
2A - A = 22023 - 21
A = 22023 - 2
b, A + 2 = 2\(^x\) ⇒ 22023 - 2 + 2 = 2\(x\)
22023 = 2\(^x\)
2023 = \(x\)
30 tháng 6 2019
Bài làm
x = \(\frac{20}{21}+\frac{21}{22}+\frac{22}{23}+\frac{23}{20}\)
x = 1 + 1 + 1 + 1 + \((\)\(\frac{3}{20}-\frac{1}{21}-\frac{1}{22}-\frac{1}{23})\)
Ta thấy 0 < \(\frac{3}{20}-\frac{1}{21}-\frac{1}{22}-\frac{1}{23}\)
\(\Rightarrow\) 1 + 1 + 1 + 1 + \((\frac{3}{20}-\frac{1}{21}-\frac{1}{22}-\frac{1}{23})\)> 4
\(\Rightarrow\)x > 4
CC
2
LN
24 tháng 7 2017
a) x. (22+23)=90
x.45=90
x=90:45
x=2
b)2x+293=309
2x=309-293
2x=16
x=16:2
x=8
NM
2
24 tháng 5 2023
21 + 22 + 23 + 24 + 25 + ... + x = 4840
=> [ (x-21) :1+1 ] . ( x+21):2= 4840
=> ( x-20) . (x+21)= 9680
=> x2 +x - 420 = 9680
<=> x2 +n - 100100 = 0
=> x(x−100)+101(x−100)=0
⇔(x +101)(x −100)=0
<=> x=−101(loại)
x =100 ( chọn)
=> x=100
Vậy x = 100
24 tháng 5 2023
Ta có: $21 + 22 + 23 + 24 + 25 + … + x = \sum_{i=21}^{x} i$
Sử dụng công thức tính tổng của dãy số liên tiếp, ta có:
$\sum_{i=21}^{x} i = \dfrac{(21 + x)(x - 21 + 1)}{2} = \dfrac{(x + 21)(x - 20)}{2}$
Vậy $\dfrac{(x + 21)(x - 20)}{2} = 4840$
$\Leftrightarrow (x + 21)(x - 20) = 9680$
$\Leftrightarrow x^2 + x - 420 = 0$
Áp dụng công thức tính nghiệm của phương trình bậc hai, ta có:
$x = \dfrac{-1 \pm \sqrt{1 + 4 \times 420}}{2} = \dfrac{-1 \pm 41}{2}$
Vì $x > 21$ nên ta chọn $x = \dfrac{-1 + 41}{2} = 20$
Vậy kết quả là $x = 42$.
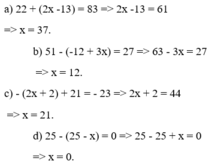
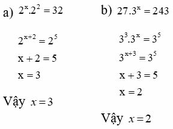
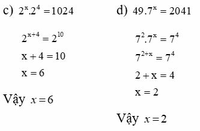
21 x 22 x 23 x ... x 2x = 1024
=> 21+2+3+...+x = 210
=> 1 + 2 + 3 + ... + x = 10
=> (1 + x).x:2 = 10
=> (1 + x).x = 10.2
=> (1 + x).x = 20
=> (1 + x).x = 5.4
=> x = 4
Vậy x = 4
X=4 nha bạn