Viết dưới dạng số thập phân các số sau:
a. 35%= b. 90
45% 75%
55% 60%
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phân số hữu hạn là : \(\frac{5}{8}=0.625,-\frac{3}{20}=-0.15\)\(\frac{14}{35}=\frac{2}{5}=0.4\) vì mẫu tối giản của chúng là tích của các lũy thừa 2 và 5.
Phân số còn lại là vô hạn tuần hoàn vì mẫu của chúng không phân tích được thành tích của các lúy thừa 2 và 5.
Số \(\frac{4}{11}=0.\left(36\right),\frac{15}{22}=0.68\left(18\right),-\frac{7}{12}=-0.58\left(3\right)\)

+ 8 = 23 chỉ có ước nguyên tố là 2
⇒ 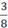 viết được dưới dạng số thập phân hữu hạn.
viết được dưới dạng số thập phân hữu hạn. 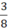 = 0,375
= 0,375
+ 5 chỉ có ước nguyên tố là 5
⇒ 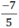 viết được dưới dạng số thập phân hữu hạn.
viết được dưới dạng số thập phân hữu hạn. 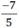 = -1,4
= -1,4
+ 20 = 22.5 có ước nguyên tố là 2 và 5.
⇒ 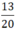 viết được dưới dạng số thập phân hữu hạn.
viết được dưới dạng số thập phân hữu hạn. 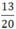 = 0,65
= 0,65
+ 125 = 53 chỉ có ước nguyên tố là 5.
⇒ 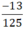 viết được dưới dạng số thập phân hữu hạn.
viết được dưới dạng số thập phân hữu hạn. 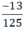 = -0,104
= -0,104


1 4 = 25 100 = 0 , 25 3 5 = 6 10 = 0 , 6 7 8 = 7 . 125 8 . 125 = 875 1000 = 0 , 875 1 2 = 5 10 = 0 , 5 Vậy 1 1 2 = 1 , 5

a) Các phân số được viết dưới dạng tối giản là:
\(\dfrac{5}{8};\dfrac{-3}{20};\dfrac{4}{11};\dfrac{15}{22};\dfrac{-7}{12};\dfrac{2}{5}\)
Lần lượt xét các mẫu:
8 = 23; 20 = 22.5 11
22 = 2.11 12 = 22.3 35 = 7.5
+ Các mẫu không chứa thừa số nguyên tố nào khác 2 và 5 là 8; 20; 5 nên các phân số viết dưới dạng số thập phân hữu hạn.
Kết quả là:
\(\dfrac{5}{8}=0,625\) \(\dfrac{-3}{20}=-0,15\) \(\dfrac{14}{35}=\dfrac{2}{5}=0,4\)
+ Các mẫu có chứa thừa số nguyên tố khác 2 và 5 là 11, 22, 12 nên các phân số viết dưới dạng số thập phân vô hạn tuần hoàn.
Kết quả là:
\(\dfrac{4}{11}=0,\left(36\right)\) \(\dfrac{-3}{20}=0,6\left(81\right)\) \(\dfrac{-7}{12}=-0,58\left(3\right)\)
b) Các phân số được viết dạng số thập phân hữu hạn
\(\dfrac{5}{8}=0,625\) \(\dfrac{-3}{20}=0,15\) \(\dfrac{14}{35}=0,4\)
Các số thập phân vô hạn tuần hoàn là:
\(\dfrac{15}{22}=0,6\left(81\right)\) \(\dfrac{-7}{12}=-0,58\left(3\right)\) \(\dfrac{4}{11}=0,\left(36\right)\)
a) Các phân số được viết dưới dạng tối giản là:
58;−320;411;1522;−712;2558;−320;411;1522;−712;25.
Lần lượt xét các mẫu:
8 = 23; 20 = 22.5 11
22 = 2.11 12 = 22.3 35 = 7.5
+ Các mẫu không chứa thừa số nguyên tố nào khác 2 và 5 là 8; 20; 5 nên các phân số viết dưới dạng số thập phân hữu hạn.
Kết quả là:
58=0,625;58=0,625; −320=−0,15−320=−0,15; 1435=25=0,41435=25=0,4
+ Các mẫu có chứa thừa số nguyên tố khác 2 và 5 là 11, 22, 12 nên các phân số viết dưới dạng số thập phân vô hạn tuần hoàn.
Kết quả là:
411=0,(36)411=0,(36) 1522=0,6(81)1522=0,6(81) −712=0,58(3)−712=0,58(3)
b) Các phân số được viết dạng số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn là:
58=0,62558=0,625 −320=−0,15−320=−0,15 411=0,(36)411=0,(36)
1522=0,6(81)1522=0,6(81) −712=0,58(3)−712=0,58(3) 1435=0,4
\(a)\)
\(35\text{%}\)\(=\frac{35}{100}=0,35\)
\(45\%=\frac{45}{100}=0,45\)
\(60\%=\frac{60}{100}=0,6\)
\(55\%=\frac{55}{100}=0,55\)
\(b)\)
\(90\%=\frac{90}{100}=0,9\)
\(75\%=\frac{75}{100}=0,75\)
a)
35% = 0,35
45% = 0,45
55% = 0,55
b)
90% = 0,9
75% = 0,75
60% = 0,6