Cho tam giác ABC vuông tại A, đường cao AH.
a, ∆ABC ᔕ ∆ABH
b, Cho AB = 4cm, AC = 5cm. Tính BH
Các bạn giúp mik câu b vs, trình bày chi tiết chút ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 8 2023
3:
ΔAHB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔAHC vuông tại H có HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
MT
22 tháng 7 2018
BÀI 1:
a)
· Trong ∆ ABC, có: AB2= BC.BH
Hay BC= 
= 
· Xét ∆ ABC vuông tại A, có:
AB2= BH2+AH2
↔AH2= AB2 – BH2
↔AH= 
=4 (cm)
b)
· Ta có: HC=BC-BH
àHC= 8.3 - 3= 5.3 (cm)
· Trong ∆ AHC, có:
· 
KT
22 tháng 7 2018
Bài 1:
a) Áp dụng hệ thức lượng ta có:
\(AB^2=BH.BC\)
\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)
\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)
Áp dụng Pytago ta có:
\(AH^2+BH^2=AB^2\)
\(\Rightarrow\)\(AH^2=AB^2-BH^2\)
\(\Rightarrow\)\(AH^2=5^2-3^2=16\)
\(\Rightarrow\)\(AH=4\)
b) \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)
Áp dụng hệ thức lượng ta có:
\(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)
\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)
\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)
\(\Rightarrow\)\(HE=\frac{16}{5}\)
28 tháng 7 2015
bạn hỏi nhiều quá , các bạn nhìn vào ko biết trả lời sao đâu !!!
CL
13 tháng 2 2016
rối mắt quá mà viết dày nên bài nọ xọ bài kia mình ko trả lời được cho dù biết rất rõ
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 6 2023
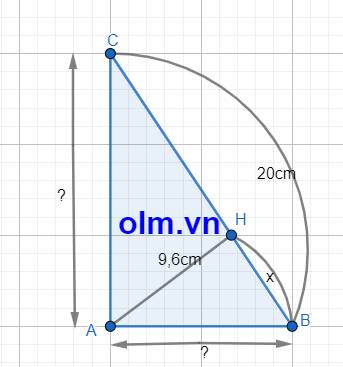
Gọi độ dài đoạn BH là: \(x\) ( cm) ; \(x\) > 0; AC > AB nên \(x\) < CH
Xét tam giác vuông HAB vuông tại H theo pytago ta có:
AB2 = HA2 + HB2 = 9,62 + \(x^2\) = 92,16 + \(x^2\)
Xét tam giác vuông AHC vuông tại H theo pytago ta có:
AC2 = HA2 + HC2 = 9,62 + (\(20-x\))2 = 92,16 + 400 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(x\) + \(x^2\)
Xét tam giác vuông ABC vuông tại A theo pytago ta có:
AC2 + AB2 = BC2
492,16 - 40\(x\) + \(x^2\) + 92,16 + \(x^2\) = 202
(\(x^2\) + \(x^2\)) - 40\(x\) + (492,16 + 92,16) - 400 = 0
2\(x^2\) - 40\(x\) + 584,32 - 400 = 0
2\(x^2\)- 40\(x\) + 184,32 =0
\(x^2\) - 20\(x\) + 92,16 = 0
△' = 102 - 92,16 = 7,84 > 0
\(x\)1 = -(-10) + \(\sqrt{7,84}\) = 12,8 ⇒ CH = 20 - 12,8 = 7,2 < BH (loại )
\(x_2\) = -(-10) - \(\sqrt{7,84}\) = 7,2 ⇒ CH = 20 - 7,2 = 12,8 (thỏa mãn)
Thay \(x_2\) = 7,2 vào biểu thức: AB2 = 92,16 + \(x^2\) = 92,16 + 7,22 = 144
⇒AB = \(\sqrt{144}\) = 12
Thay \(x_2\) = 7,2 vào biểu thức: AC2 = 492,16 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(\times\) 7,2 + 7,22 = 256
AC = \(\sqrt{256}\) = 16
Kết luận AB = 12 cm; AC = 16 cm
AH
Akai Haruma
Giáo viên
21 tháng 8 2023
Lời giải:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
Áp dụng hệ thức lượng trong tam giác vuông:
$BH=\frac{AB^2}{BC}=\frac{3^2}{5}=\frac{9}{5}=1,8$ (cm)
$CH=BC-BH=5-1,8=3,2$ (cm)
$\frac{BD}{CD}=\frac{AB}{AC}=\frac{3}{4}$
$\Rightarrow \frac{BD}{BD+CD}=\frac{3}{7}$
Hay $\frac{BD}{BC}=\frac{3}{7}\Rightarrow BD=\frac{3}{7}.BC=\frac{3}{7}.5=\frac{15}{7}$ (cm)
$CD=BC-BD=5-\frac{15}{7}=\frac{20}{7}$ (cm)
$HD=BD-BH=\frac{15}{7}-1,8=\frac{12}{35}$ (cm)
4 tháng 8 2016
Câu 1:
Áp dụng đ/lí pytago vào tam giác ABC vuông tại A CÓ:AB^2+AB^2=BC^2
Hay: 12^2+5^2=169=BC^2
=> BC=13cm
ÁP dụng hệ thức ta có:
+) AB^2=BH.BC
Hay: BH=AB^2:BC=144:13 =144/13(cm)
Ta có CH=BC-BH=13-144/13=25/13(cm)
H9
HT.Phong (9A5)
CTVHS
17 tháng 6 2023
Xét \(\Delta ABC\) và \(\Delta HBA\) có:
\(\widehat{BAC}=\widehat{BHA}=90^o\)
\(\widehat{B}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\) (1)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{HB}{AB}\) hay \(\dfrac{AB}{4+9}=\dfrac{4}{AB}\Rightarrow AB^2=52\Rightarrow AB=\sqrt{52}=2\sqrt{13}cm\)
Xét \(\Delta\text{A}BC\) và \(\Delta HAC\) có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{C}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g.g\right)\) (2)
Từ (1) và (2) \(\Rightarrow\Delta HAB\sim\Delta HCA\)
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{HB}{AH}\) hay \(\dfrac{AH}{9}=\dfrac{4}{AH}\Rightarrow AH^2=36\Rightarrow AH=\sqrt{36}=6\left(cm\right)\)
Ta có \(\Delta ABC\) vuông tại A.
Áp dụng đinh lý Py-ta-go ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{\left(4+9\right)^2-\left(2\sqrt{13}\right)^2}=3\sqrt{13}cm\)
b) Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot AH=\dfrac{1}{2}\cdot\left(4+9\right)\cdot6=39\left(cm^2\right)\)
Bạn tự vẽ hình nhé!
a, Xét \(\Delta ABC.và.\Delta ABH.có:\)
\(\widehat{BAC}=\widehat{BHA}\)
\(\widehat{B}.chung\)
\(\Rightarrow\Delta ABC\sim\Delta ABH\)
b, Áp dụng định lý Pytago vào tam giác vuông ABC, ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=4^2+5^2=41\\ \Rightarrow BC=\sqrt{41}\approx6,4\left(cm\right)\)
Vì \(\Delta ABC\sim\Delta ABH\) và \(\Delta ABC\) có đường cao AH:
\(\Rightarrow\dfrac{BH}{BA}=\dfrac{HC}{AC}\) ( 1 )
Dựa vào tính chất dãy tỉ số bằng nhau, ta lại có:
\(\left(1\right)\Rightarrow\dfrac{BH}{BA}=\dfrac{HC}{AC}=\dfrac{BH+HC}{BA+AC}=\dfrac{BC}{4+5}=\dfrac{6,4}{9}\)
\(\Rightarrow BH=\dfrac{4.6,4}{9}=2,8\left(cm\right)\)