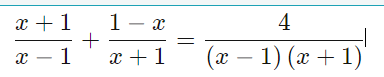
tìm đkxd và giải pt .hứa vote nhanh ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
31 tháng 1 2023
Bài 1:
$2x^4-3x^2-5=0$
$\Leftrightarrow (2x^4+2x^2)-(5x^2+5)=0$
$\Leftrightarrow 2x^2(x^2+1)-5(x^2+1)=0$
$\Leftrightarrow (x^2+1)(2x^2-5)=0$
$\Leftrightarrow 2x^2-5=0$ (do $x^2+1\geq 1>0$ với mọi $x\in\mathbb{R}$)
$\Leftrightarrow x^2=\frac{5}{2}$
$\Leftrightarrow x=\pm \sqrt{\frac{5}{2}}$
AH
Akai Haruma
Giáo viên
31 tháng 1 2023
Bài 2:
a. Khi $m=1$ thì pt trở thành:
$x^2-6x+5=0$
$\Leftrightarrow (x^2-x)-(5x-5)=0$
$\Leftrightarrow x(x-1)-5(x-1)=0$
$\Leftrightarrow (x-1)(x-5)=0$
$\Leftrightarrow x-1=0$ hoặc $x-5=0$
$\Leftrightarrow x=1$ hoặc $x=5$
b.
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta=(m+5)^2-4(-m+6)\geq 0$
$\Leftrightarrow m^2+14m+1\geq 0(*)$
Áp dụng định lý Viet:
$x_1+x_2=m+5$
$x_1x_2=-m+6$
Khi đó:
$x_1^2x_2+x_1x_2^2=18$
$\Leftrightarrow x_1x_2(x_1+x_2)=18$
$\Leftrightarrow (m+5)(-m+6)=18$
$\Leftrightarrow -m^2+m+12=0$
$\Leftrightarrow m^2-m-12=0$
$\Leftrightarrow (m+3)(m-4)=0$
$\Leftrightarrow m=-3$ hoặc $m=4$
Thử lại vào $(*)$ thấy $m=4$ thỏa mãn.
31 tháng 7 2023
4.3:
a: Xét ΔCED vuông tại E và ΔCAB vuông tại A có
góc C chung
=>ΔCED đồng dạng với ΔCAB
b: ΔCED đồng dạng với ΔCAB
=>ED/AB=EC/AC
=>ED*AC=EC*AB
c: BC=căn 9^2+12^2=15cm
AD là phân giác
=>DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=15/7
=>DC=60/7cm
29 tháng 7 2023
ĐKXĐ: x^2-5x+6>=0 và x^2-2<>0
=>(x>=3 hoặc x<=2) và (x<>căn 2 và x<>-căn 2)
=>x>=3 hoặc \(\left\{{}\begin{matrix}x< =2\\x\notin\left\{\sqrt{2};-\sqrt{2}\right\}\end{matrix}\right.\)
NN
13 tháng 10 2020
1. \(S=1+3+3^2+3^3+........+3^{2019}+3^{2020}\)
\(\Rightarrow3S=3+3^2+3^3+3^4+........+3^{2020}+3^{2021}\)
\(\Rightarrow3S-S=3^{2021}-1\)
\(\Rightarrow2S=3^{2021}-1\)
\(\Rightarrow S=\frac{3^{2021}-1}{2}\)
2. \(\left(3x-2\right)^3=64\)
\(\Leftrightarrow\left(3x-2\right)^3=4^3\)
\(\Leftrightarrow3x-2=4\)
\(\Leftrightarrow3x=6\)
\(\Leftrightarrow x=2\)
Vậy \(x=2\)
PH
14 tháng 10 2020
[3x-2]^3=64
Ta có:64=4^3
Suy ra:3x-2=4
3x =4+2
3x=6
x=6:3
x=2
8 tháng 1 2021
a) Xác định bài toán
-Input: Dãy n số
-Output: Các số nguyên khác 0
b) Biểu diễn thuật toán
-Bước 1: Nhập n và nhập dãy số
-Bước 2: i←1;
-Bước 3: Nếu a[i]<>0 thì xuất a[i]
-Bước 4: i←i+1;
-Bước 5: Nếu i<=n thì quay lại bước 3
-Bước 6: Kết thúc
H
0
A
28 tháng 10 2021
Tham khảo
+ HAVE TO diễn tả nghĩa “phải” do xuất phát từ chủ quan người nói. Ví dụ: I have to brush my teeth twice a day.
+ MUST chỉ dùng được cho thì hiện tại hoặc tương lai, nhưng nếu muốn diễn tả ý nghĩa “phải” trong quá khứ, ta phải sử dụng
Have To. Ví dụ: I had to go to the dentist yesterday.
NH
1
9 tháng 10 2021
Bài 7:
Ta có: \(P=\left(\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right):\left(1+\dfrac{\sqrt{x}}{x+1}\right)\)
\(=\dfrac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{x+1}{x+\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}}{x\sqrt{x}-1}\)
28 tháng 10 2021
Bài 2:
a: \(6.25\cdot1.34=8.375\)
b: \(48.6\cdot2.5=121.5\)
\(\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\left(ĐKXĐ:x\ne1;x\ne-1\right)\)
\(\Leftrightarrow\left(x+1\right)\left(x+1\right)+\left(1-x\right)\left(x-1\right)=4\)
\(\Leftrightarrow x^2+x+x+1+x-1-x^2+x=4\)
\(\Leftrightarrow x^2-x^2+x+x+x+x-4+1-1=0\)
\(\Leftrightarrow4x-4=0\)
\(\Leftrightarrow4x=4\)
\(\Leftrightarrow x=1\left(loại\right)\)
Vậy \(S=\varnothing\)
\(\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{\left(1-x\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1\right)^2-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{\left(x+1+x-1\right)\left(x+1-x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{2x.2}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇔ \(\dfrac{4x}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\)
⇒ \(4x=4\)
⇔ \(x=1\) (ko thỏa mãn dktc)
Vậy phương trình vô nghiệm