Số sánh 72^24- 72^23 và 72^23- 72^22
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BH
3
19 tháng 8 2018
P/s : mk làm phần b trước
\(6\cdot5^{22}=\left(5+1\right)\cdot5^{22}=5^{23}+5^{22}>5^{23}\)
Hok tốt
19 tháng 8 2018
a) đây :
\(72^{45}-72^{44}=72^{44}\cdot72-72^{44}=72^{44}\cdot\left(72-1\right)\)
\(72^{44}-72^{43}=72^{43}\cdot72-72^{43}=72^{43}\cdot\left(72-1\right)\)
mà \(72^{44}>72^{43}\)=> \(72^{44}\cdot\left(72-1\right)>72^{43}\cdot\left(72-1\right)\)
=> \(72^{45}-72^{44}>72^{44}-72^{43}\)
LT
2
D
23 tháng 9 2017
a. Ta có: \(5^{36}=\left(5^3\right)^{12}=125^{12}\)
\(11^{24}=\left(11^2\right)^{12}=121^{12}\)
\(Do\)\(125^{12}>121^{12}\Rightarrow5^{36}>11^{24}\)
b) Ta có; \(6.5^{22}>5.5^{22}=5^{23}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
26 tháng 12 2016
a/ \(27^{11}=\left(3^3\right)^{11}=3^{33}\); \(81^8=\left(3^4\right)^8=3^{32}< 3^{33}\Rightarrow81^8< 27^{11}\)
b/ \(3^{2n}=\left(3^2\right)^n=9^n\); \(2^{3n}=\left(2^3\right)^n=8^n< 9^n\Rightarrow2^{3n}< 3^{2n}\)
26 tháng 6 2018
a. 2711= (33)11 = 333
818 = (34)8 = 332
Suy ra 333>332 hay 2711>818
b. 32n = (32)n = 9n
23n = (23)n = 8n
Mà 9>8 suy ra 9n>8n hay 32n>23n
c. 523 = 522 . 5
(6.5)22 = 622 . 522
Vì 622>5 suy ra 522 . 5<622 . 522 hay 523<(6.5)22
d. 7245-7244 = 7244(72-1) = 7244 . 71
7244-7243 = 7243(72-1) = 7243 . 71
Vì 7244>7243 suy ra 7244 . 71>7243 . 71 hay 7245-7244>7244-7243
25 tháng 12 2016
a) Ta có: 2711= (33)11=333
818=(34)8=332
Suy ra: 2711>818
Mình chỉ làm cho bn 1 ví dụ thôi. các bài còn lại bn làm tương tự nhé!
CM
11 tháng 10 2019
Đáp án là A
Ta có: M = 14 - 23 + (5 - 14) - (5 - 23) + 17 = 14 - 23 + 5 - 14 - 5 + 23 + 17
= (14 - 14) + (5 - 5) - (23 - 23) + 17 = 0 + 0 - 0 + 17 = 17
N = 24 - (72 - 13 + 24) - (72 - 13) = 24 - 72 + 13 - 24 - 72 + 13
= (24 - 24) - (72 + 72) + (13 + 13) = 0 - 144 + 26 = -118
Do đó M > N
N
So sánh:
d) 2^13 và 2^16
e) 21^15 và 27^5.49^8
f) 72^45-72^44 và 72^44- 72^23
Cần gấp mn ơi
Cảm ơn 🥺
0
N
So sánh:
d) 2^13 và 2^16
e) 21^15 và 27^5.49^8
f) 72^45-72^44 và 72^44- 72^23
Cần gấp mn ơi
Cảm ơn 🥺
0
PA
1
30 tháng 10 2021
72-8x9 bằng 0 chia 20 cộng 21 cộng 22 cộng 23 cộng 24 cộng 25 bằng 128
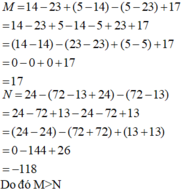
72^24-72^23=72^23(72-1)=71.72^23
72^23-72^22=72^22(72-1)=72^22.71