Cho đường tròn \(\left(C\right)\) tâm \(I\) , bán kính bằng 2. Điểm \(M\in\Delta:x+y=0\) . Từ \(M\) kẻ hai tiếp tuyến \(MA,MB\) đến \(\left(C\right)\) với \(A,B\) là tiếp điểm. \(AB:3x+y-2=0\) , \(d\left(I,\Delta\right)=2\sqrt{2}\) . Viết phương trình đường tròn \(\left(C\right)\).

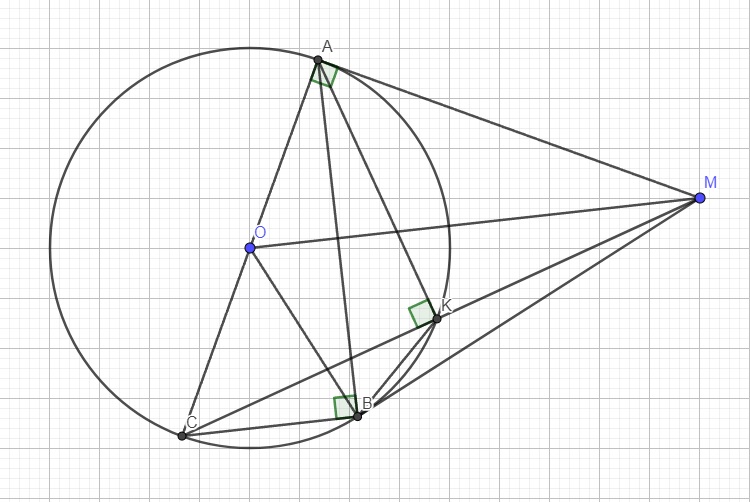
Gọi C là giao điểm của AB và \(\Delta\), O là giao điểm IM và AB
Gọi \(I=\left(m;n\right)\Rightarrow IM:x-3y-m+3n=0\)
\(M:\left\{{}\begin{matrix}x-3y-m+3n=0\\x+y=0\end{matrix}\right.\Rightarrow M=\left(\dfrac{m-3n}{4};\dfrac{3n-m}{4}\right)\)
\(\Rightarrow IM=\sqrt{\left(\dfrac{m-3n}{4}-m\right)^2+\left(\dfrac{3n-m}{4}-n\right)^2}=\dfrac{\sqrt{10}\left|m+n\right|}{4}\)
\(d\left(I,\Delta\right)=\dfrac{\left|m+n\right|}{\sqrt{2}}=2\sqrt{2}\Rightarrow\left|m+n\right|=4\left(1\right)\)
\(\Rightarrow IM=\sqrt{10}\)
Ta có \(IO.IM=IA^2=R^2\Rightarrow IO=\dfrac{IB^2}{IM}=\dfrac{4}{\sqrt{10}}\)
\(d\left(I;AB\right)=\dfrac{\left|3m+n-2\right|}{\sqrt{10}}=\dfrac{4}{\sqrt{10}}\Rightarrow\left|3m+n-2\right|=4\left(2\right)\)
Từ \(\left(1\right)\&\left(2\right)\) tìm được tọa độ điểm I
Đến đây viết phương trình đường tròn tâm I có bán kính \(R=\sqrt{2}\) là được.