Một chất điểm dao động điều hoà dọc theo trục Ox. Phương trình dao động là x = 5cos(πt+π/6) cm. Quãng đường vật đi từ thời điểm ban đầu tới thời điểm t = 343/36 s là
A. 100,437 cm. B. 97,198 cm. C. 96,462 cm. D. 89, 821cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
10 tháng 6 2018
Đáp án B
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
Chu kỳ dao động T = 2s
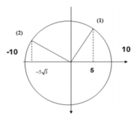
Quan sát trên hình vẽ ta thấy quãng đường vật đi được từ thời điểm t1 = 0,5s ứng với vị trí (1) đến thời điểm t2 = 1s ứng với vị trí (2) là: (5 + 5 3 ) = 13,7cm
VT
16 tháng 9 2017
Tại t = 0, vật đang ở vị trí biên âm.
Ta có S = 2,5A = 12,5 cm → vật mất khoảng thời gian
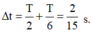
Đáp án D
VT
15 tháng 4 2018
ü Đáp án D
+ Tại t = 0, vật đang ở vị trí biên âm.
Ta có S = 2,5A = 12,5 cm → vật mất khoảng thời gian Δ t = T 2 + T 6 = 2 15 s
30 tháng 7 2016
Đáp án D
Bạn dùng vòng tròn để giải :
- Lúc t = 0 vật qua vị trí 1,5 cm theo chiều +, góc hợp với OX là \(\frac{\pi}{3}\)
- khi t = 0,157 s = \(\frac{\pi}{20}\) thì trên vòng tròn nó sẽ quét được góc \(\frac{\pi}{2}\) vậy góc hợp với trục ox là \(\frac{\pi}{6}\)
Vậy x = 1,5 \(\sqrt{3}\)
=> S = 1,5 + (3 - 1,5 \(\sqrt{3}\)) = 1,9
30 tháng 7 2016
\(T=\frac{2\pi}{\omega}=\frac{157}{250}s\)
\(\Delta t=\frac{157}{1000}=\frac{T}{4}=\frac{T}{12}+\frac{T}{6}\)
Tại thời điểm t=0s vật ở vị trí \(x=\frac{A}{2}=1,5cm\) đi theo chiều âm của trục tọa độ.
Vậy quãng đường vật đi được là
\(S=\frac{A}{2}+\frac{A\sqrt{3}}{2}=\frac{3+3\sqrt{3}}{2}=4,098\approx4,1\) cm
Vậy C đúng
