giúp mih với ạa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Carlo Nobix là một cậu bé đầy kiêu hãnh về xuất thân giàu có và người cha quyền quý của mình. Trong một lần xích mích với Betty - con của một người bán than cậu đã nói rằng "Bố mày là đồ bạn tiện". Betty tức giận và về kể lại cho bố. Sau đó bố của Betty đã đến trường phàn nàn với thầy giáo và đúng lúc bố của Carlo đến nơi. Sau khi biết được câu chuyện, bố Carlo đã nghiêm khắc bắt con trai mình nói lời xin lỗi. Carlo bắt buộc phải lặp lại lời xin lỗi. Rôi bố của Carlo bắt tay một cách nồng nàn với bố của Betty. Đồng thời ông yêu cầu thầy giáo để hai đứa trẻ ngồi cạnh nhau. Sau một lúc do dự, ông hàng than tiến tới lấy đôi bàn tay chuối hột vuốt tóc ông Carlo rồi đi thẳng. Thầy giáo dặn những đứa trẻ vừa rồi chính là bài học hay nhất trong năm.


Ta có: \(n_{SO_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\)
a. PTHH:
Na2SO3 + H2SO4 ---> Na2SO4 + SO2 + H2O (1)
K2SO3 + H2SO4 ---> K2SO4 + SO2 + H2O (2)
Theo PT(1,2): \(n_{H_2SO_4}=n_{SO_2}=0,3\left(mol\right)\)
=> \(m_{H_2SO_4}=0,3.98=29,4\left(g\right)\)
b. Gọi x, y lần lượt là số mol của Na2SO3 và K2SO3
Theo PT(1,2):
=> x + y = 0,3
Theo đề, ta có: 126x + 158y = 44,2
=> x = 0,1, y = 0,2
Theo PT(1): \(n_{Na_2SO_4}=n_{Na_2SO_3}=0,1\left(mol\right)\)
=> \(m_{Na_2SO_4}=0,1.142=14,2\left(g\right)\)
Theo PT(2): \(n_{K_2SO_4}=n_{K_2SO_3}=0,2\left(mol\right)\)
=> \(m_{K_2SO_4}=0,2.164=34,8\left(g\right)\)
=> \(m_{sau.phản.ứng}=34,8+14,2=49\left(g\right)\)
Ta có: \(C_{\%_{H_2SO_4}}=\dfrac{0,3.98}{m_{dd_{H_2SO_4}}}.100\%=20\%\)
=> \(m_{dd_{H_2SO_4}}=147\left(g\right)\)
Ta có: \(m_{dd_{sau.phản.ứng}}=147+44,2=191,2\left(g\right)\)
=> \(C_{\%_{dd_{sau.phản.úng}}}=\dfrac{49}{191,2}.100\%=25,63\%\)
c. Đổi 500ml = 0,5 lít
=> \(n_{Ba\left(OH\right)_2}=1.0,5=0,5\left(mol\right)\)
Ta có: \(T=\dfrac{n_{SO_2}}{n_{Ba\left(OH\right)_2}}=\dfrac{0,3}{0,5}=0,6< 1\)
Vậy PTHH là: \(SO_2+Ba\left(OH\right)_2--->BaSO_3+H_2O\) (Ba(OH)2 dư.)
Theo PT: \(n_{BaSO_3}=n_{SO_2}=0,3\left(mol\right)\)
=> \(m_{BaSO_3}=0,3.217=65,1\left(g\right)\)
\(n_{SO_2}=\dfrac{6,72}{22,4}=0,3mol\)
\(Na_2SO_3+H_2SO_4\rightarrow Na_2SO_4+H_2O+SO_2\)
\(x\) \(x\)
\(K_2SO_3+H_2SO_4\rightarrow K_2SO_3+H_2O+SO_2\)
\(y\) \(y\)
Ta có: \(\left\{{}\begin{matrix}126x+158y=44,2\\x+y=0,3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=0,1\\y=0,2\end{matrix}\right.\)
a)\(\Rightarrow\Sigma n_{H_2SO_4}=0,1+0,2=0,3mol\)
\(\Rightarrow m_{H_2SO_4}=0,3\cdot98=29,4\left(g\right)\)
\(\Rightarrow m_{ddH_2SO_4}=\dfrac{29,4}{20}\cdot100=147\left(g\right)\)
b)


Hướng dẫn:
Ta có:
\(x^2-xy+y^2=2x-3y-2\)
\(\Leftrightarrow2x^2-2xy+2y^2-4x+6y+4+9=9\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2-4x+4\right)+\left(y^2+6y+9\right)=9\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-2\right)^2+\left(y+3\right)^2=9\)
Xét....
Đây là 1 cách nhưng làm hơi dài.
\(x^2-xy+y^2=2x-3y-2\\ \Leftrightarrow x^2-xy+y^2-2x+3y+2=0\left(1\right)\\ \Leftrightarrow x^2-x\left(y+2\right)+y^2+3y+2=0\)
Coi đây là pt bậc 2 ẩn x
Ta có: \(\Delta=\left[-\left(y+2\right)\right]^2-4\left(y^2+3y+2\right)=y^2+4y+4-4y^2-12y-8=-3y^2-8y-4\)
Để pt có nghiệm nguyên thì \(\Delta\ge0\Leftrightarrow-3y^2-8y-4\ge0\Leftrightarrow-2\le y\le-\dfrac{2}{3}\)
\(\Leftrightarrow y\in\left\{-2;-1\right\}\)
Thay y=-2 vào (1) ta có:
\(\left(1\right)\Leftrightarrow x^2-x.\left(-2\right)+\left(-2\right)^2-2x+3.\left(-2\right)+2=0\\ \Leftrightarrow x^2+2x+4-2x-6+2=0\\ \Leftrightarrow x^2=0\Leftrightarrow x=0\)
Thay y=-1 vào pt ta có:
\(\left(1\right)\Leftrightarrow x^2-x.\left(-1\right)+\left(-1\right)^2-2x+3.\left(-1\right)+2=0\\ \Leftrightarrow x^2+x+1-2x-3+2=0\\ \Leftrightarrow x^2-x=0\\ \Leftrightarrow x\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(0;-2\right);\left(0;-1\right);\left(1;-1\right)\right\}\)

a: 5 không là số nguyên tố
b: 4+x>=3
c: (căn 3+căn 12)^2 là số vô tỉ
d: Phương trình x^2+2023x=1 có nghiệm
e: 3^2+4^2<>5^2
f: căn 3*căn 27<>9
g: x=1 không là nghiệm của phương trình \(\dfrac{x^2-1}{x-1}=0\)
h: Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại


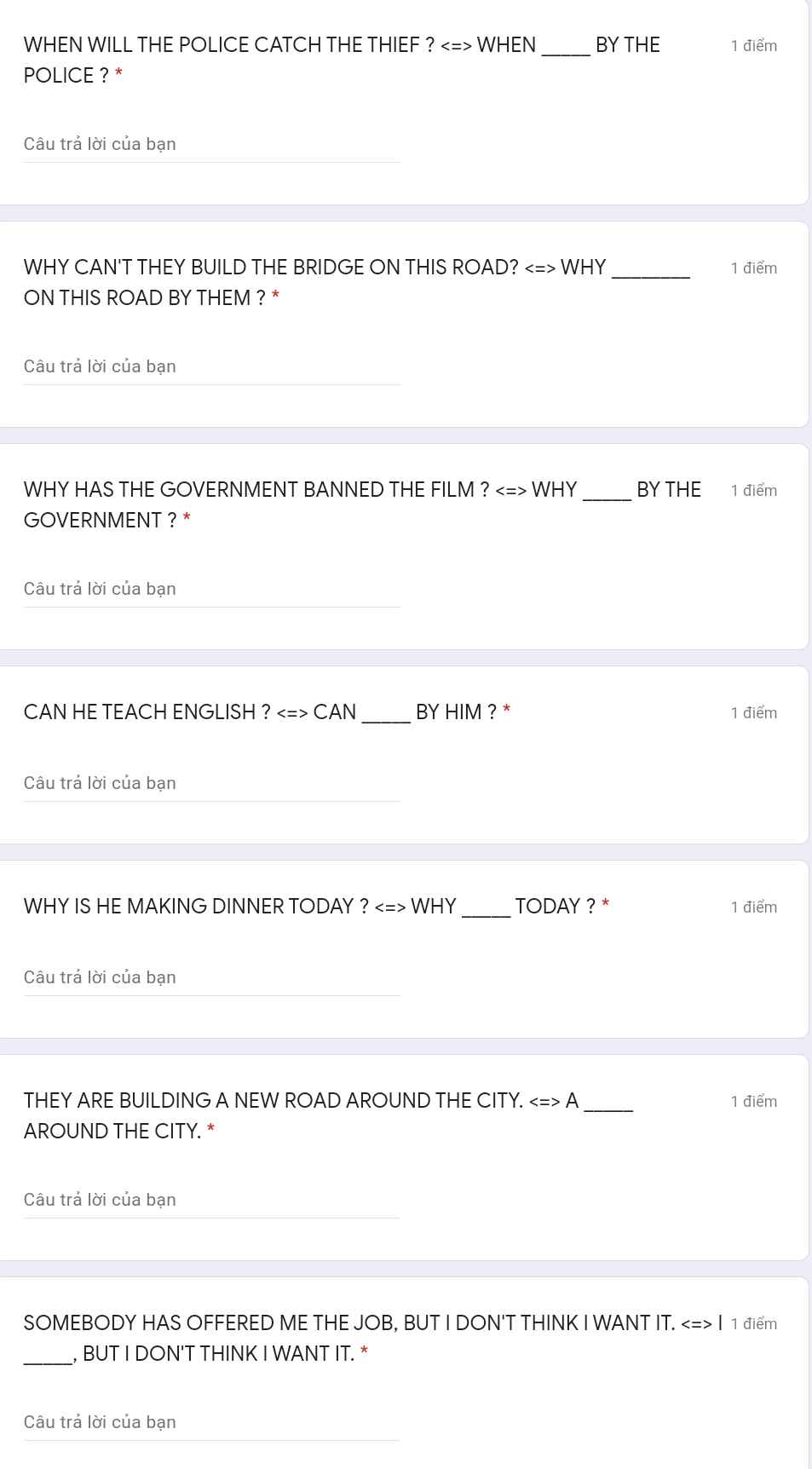 giúp em với ạa, bài này là bài tập không phải thi đâu ạa
giúp em với ạa, bài này là bài tập không phải thi đâu ạa giúp với ạa
giúp với ạa
 giúp em với ạa
giúp em với ạa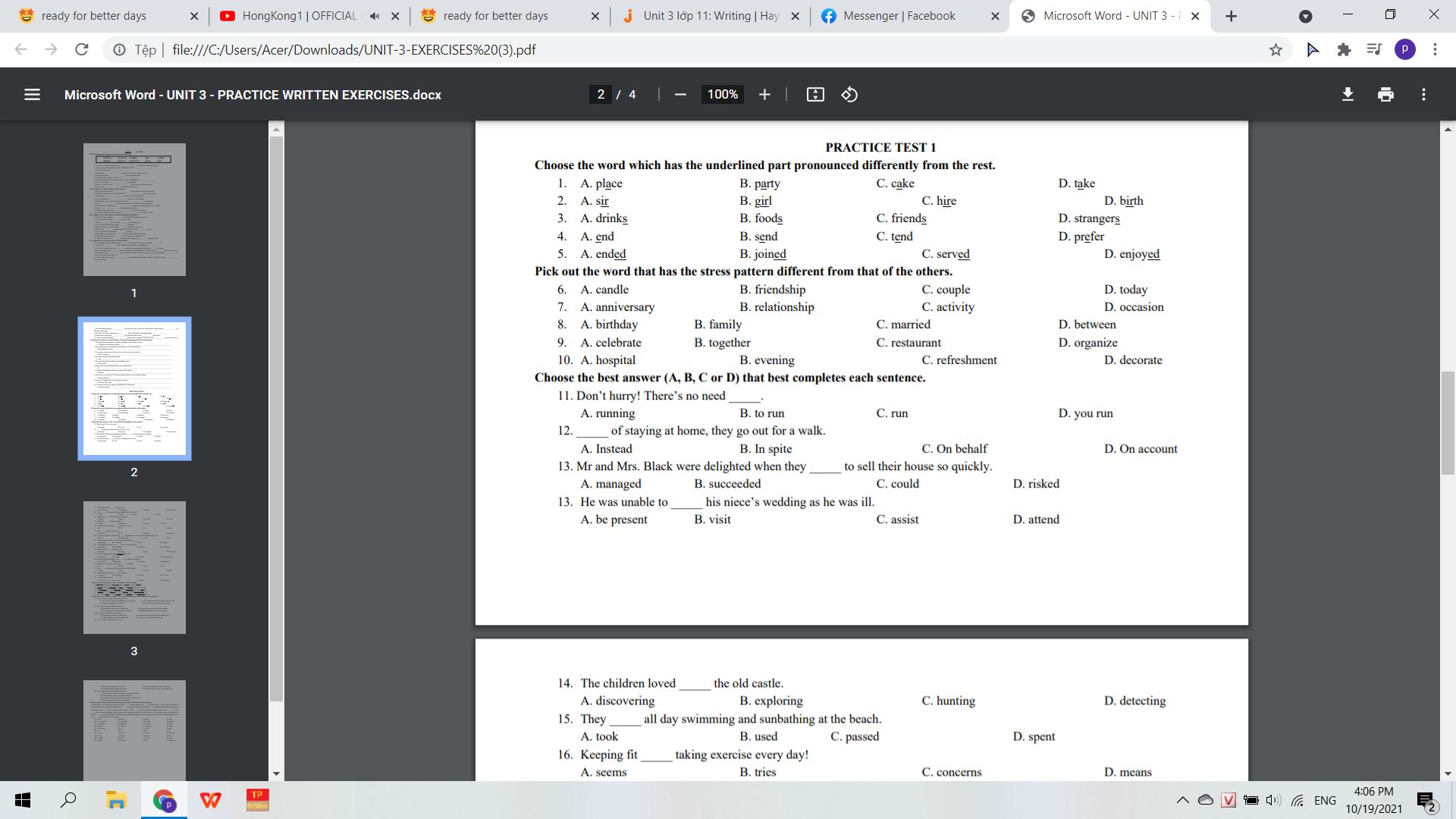
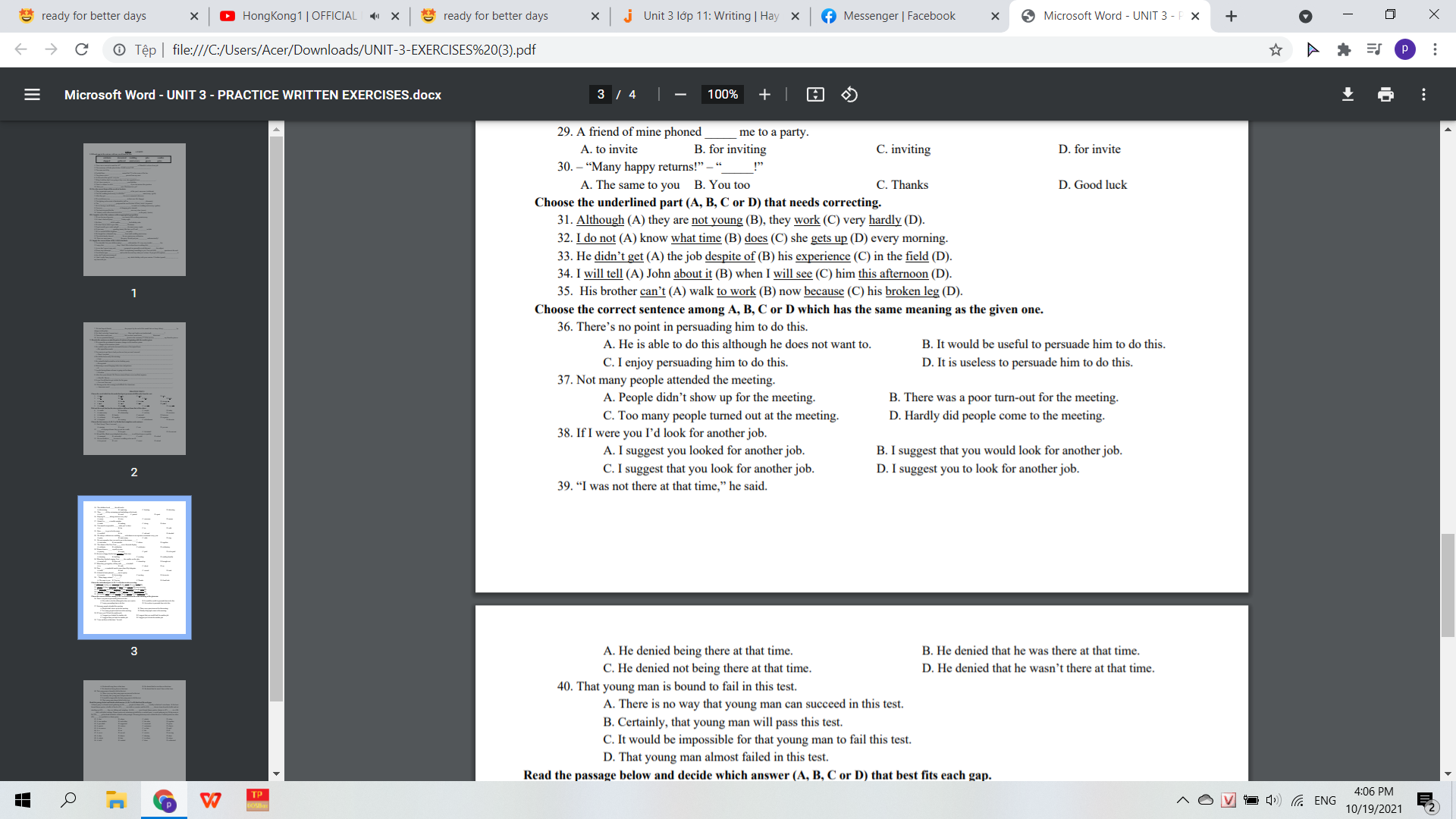

 giúp e với ạa
giúp e với ạa

Gọi vận tốc thực của ca nô và vận tốc dòng nước lần lượt là \(x;y\left(x>y>0\right)\)
Vận tốc xuôi dòng của ca nô là \(x+y\left(km/h\right)\)và vận tốc ngược dòng là \(x-y\left(km/h\right)\)
Lần thứ nhất, thời gian ca nô đi xuôi dòng là \(\frac{54}{x+y}\left(h\right)\)và thời gian ca nô đi ngược dòng là \(\frac{63}{x-y}\left(h\right)\)
Vì tổng thời gian cả đi lẫn về của ca nô lần thứ nhất là 5 giờ nên ta có pt \(\frac{54}{x+y}+\frac{63}{x-y}=5\)(1)
Lần thứ hai, thời gian ca nô đi xuôi dòng là \(\frac{108}{x+y}\left(h\right)\)và thời gian ca nô đi ngược dòng là \(\frac{84}{x-y}\left(h\right)\)
Vì tổng thời gian cả đi lẫn về của ca nô lần thứ hai là 8 giờ nên ta có pt \(\frac{108}{x+y}+\frac{84}{x-y}=8\)(2)
Từ (1) và (2) ta có hpt \(\hept{\begin{cases}\frac{54}{x+y}+\frac{63}{x-y}=5\\\frac{108}{x+y}+\frac{84}{x-y}=8\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{54}{x+y}+\frac{63}{x-y}=5\\\frac{54}{x+y}+\frac{42}{x-y}=4\end{cases}}\)(*)
Đặt \(\hept{\begin{cases}\frac{54}{x+y}=a\\\frac{21}{x-y}=b\end{cases}}\left(a,b>0\right)\), khi đó (*) trở thành \(\hept{\begin{cases}a+3b=5\\a+2b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}b=1\\a=2\end{cases}}\)(nhận)
\(\Rightarrow\hept{\begin{cases}\frac{54}{x+y}=2\\\frac{21}{x-y}=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=27\\x-y=21\end{cases}}\Leftrightarrow\hept{\begin{cases}x=24\\y=3\end{cases}}\)(nhận)
Vậy vận tốc thực của ca nô là 24 km/h và vận tốc dòng nước là 3 km/h