Tìm m để phương trình x2 + 2x + m – 3 = 0 có 2 nghiệm phân biệt x1, x2 thảo mãn x12 + x22 + 2(x1x2)2 =...
Đọc tiếp
Tìm m để phương trình x2 + 2x + m – 3 = 0 có 2 nghiệm phân biệt x1, x2 thảo mãn x12 + x22 + 2(x1x2)2 = 7x1x2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 1 2022
a, Thay m = -2 ta được :
x^2 + 6x + 3 = 0
\(\Leftrightarrow x=-3+\sqrt{6};x=-3-\sqrt{6}\)
b, Để pt có 2 nghiệm
\(\Delta'=\left(m-1\right)^2-\left(-m+1\right)=m^2-2m+1+m-1=m^2-m\)> 0
Theo Viet : \(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=-m+1\end{matrix}\right.\)
Ta có : \(\left(x_1+x_2\right)^2+5x_1x_2=9\)
\(\Leftrightarrow4\left(m-1\right)^2+5\left(-m+1\right)=9\)
\(\Leftrightarrow4m^2-8m+4-5m+5=9\Leftrightarrow4m^2-13m=0\)
\(\Leftrightarrow m\left(4m-13\right)=0\Leftrightarrow m=0\left(ktm\right);m=\dfrac{13}{4}\)(tm)
26 tháng 1 2022
a, Thay m=-2 vào pt ta có:
\(x^2-2\left(m-1\right)x-m+1=0\\ \Leftrightarrow x^2-2\left(-2-1\right)x-\left(-2\right)+1=0\\ \Leftrightarrow x^2+6x+3=0\\ \Leftrightarrow\left(x^2+6x+9\right)-6=0\\ \Leftrightarrow\left(x+3\right)^2-\sqrt{6^2}=0\\ \Leftrightarrow\left(x+3-\sqrt{6}\right)\left(x+3+\sqrt{6}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-3+\sqrt{6}\\x=-3-\sqrt{6}\end{matrix}\right.\)
\(b,\Delta'=\left[-\left(m-1\right)\right]^2-\left(-m+1\right)\\ =m^2-2m+1+m-1\\ =m^2-m\)
Để pt có 2 nghiệm thì \(\) \(\Delta'\ge0\Leftrightarrow m^2-m\ge0\Leftrightarrow\left[{}\begin{matrix}m\ge1\\m\le0\end{matrix}\right.\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=-m+1\end{matrix}\right.\)
\(x_1^2+x_2^2+7x_1x_2=9\\ \Leftrightarrow\left(x_1+x_2\right)^2+5x_1x_2=9\\ \Leftrightarrow\left(2m-2\right)^2+5\left(-m+1\right)=9\\ \Leftrightarrow4m^2-8m+4-5m+5-9=0\\ \Leftrightarrow4m^2-13m=0\\ \Leftrightarrow m\left(4m-13\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\left(tm\right)\\m=\dfrac{13}{4}\left(tm\right)\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2021
\(\Delta=9-4\left(-m^2+m+2\right)=4m^2-4m+1=\left(2m-1\right)^2\)
Pt có 2 nghiệm pb khi \(m\ne\dfrac{1}{2}\)
Do vai trò của 2 nghiệm là như nhau, giả sử: \(\left\{{}\begin{matrix}x_1=\dfrac{3-\left(2m-1\right)}{2}=2-m\\x_2=\dfrac{3+2m-1}{2}=m+1\end{matrix}\right.\)
\(x_1^2+x_2^2=5\Leftrightarrow\left(2-m\right)^2+\left(m+1\right)^2=5\)
\(\Leftrightarrow m^2-m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\)
CM
12 tháng 8 2019
Phương trình có hai nghiệm phân biệt x1, x2 ⇔ ∆ = 52 – 4(3m + 1) > 0 ⇔ 21 – 12m > 0
ó m < 21/12
Với m < 21/12 , ta có hệ thức x 1 + x 2 = 5 x 1 x 2 = 3 m + 1 V i e t '
⇒ | x 1 − x 2 | = ( x 1 − x 2 ) 2 = ( x 1 + x 2 ) 2 − 4 x 1 x 2 = 5 2 − 4 ( 3 m + 1 ) = 21 − 12 m = > | x 1 2 − x 2 2 | = | ( x 1 + x 2 ) ( x 1 − x 2 ) | = | 5 ( x 1 − x 2 ) | = 5 | x 1 − x 2 | = 5 21 − 12 m
Ta có: | x 1 2 − x 2 2 | = 15 ⇔ 5 21 − 12 m = 15 ⇔ 21 − 12 m = 3 ⇔ 21 − 12 m = 9 ⇔ 12 m = 12 ⇔ m = 1 (t/m)
Vậy m = 1 là giá trị cần tìm
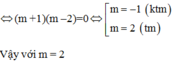
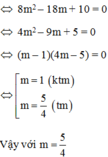
Sửa đề: \(x_1^2+x_2^2+2\left(x_1\cdot x_2\right)^2=7x_1x_2\)
Ta có: \(\Delta=2^2-4\cdot1\cdot\left(m-3\right)=4-4m+12=-4m+16\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow-4m+16>0\)
\(\Leftrightarrow-4m>-16\)
hay m<4
Khi m<4, Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1\cdot x_2=m-3\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2+2\left(x_1\cdot x_2\right)^2=7x_1x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2\cdot x_1\cdot x_2+2\left(x_1\cdot x_2\right)^2=7\cdot x_1\cdot x_2\)
\(\Leftrightarrow\left(-2\right)^2-2\cdot\left(m-3\right)+2\cdot\left(m-3\right)^2=7\left(m-3\right)\)
\(\Leftrightarrow4-2m+6+2\left(m^2-6m+9\right)=7m-21\)
\(\Leftrightarrow-2m+10+2m^2-12m+18-7m+21=0\)
\(\Leftrightarrow2m^2-21m+49=0\)
\(\Leftrightarrow2m^2-14m-7m+49=0\)
\(\Leftrightarrow2m\left(m-7\right)-7\left(m-7\right)=0\)
\(\Leftrightarrow\left(m-7\right)\left(2m-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-7=0\\2m-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=7\left(loại\right)\\2m=7\end{matrix}\right.\Leftrightarrow m=\dfrac{7}{2}\left(nhận\right)\)
Vậy: Để phương trình có hai nghiệm phân biệt thỏa mãn \(x_1^2+x_2^2+2\left(x_1\cdot x_2\right)^2=7x_1x_2\) thì \(m=\dfrac{7}{2}\)
Ta có: x2 + 2x + m - 3 = 0
Theo hệ thực Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=m-3\end{matrix}\right.\) (I)
Ta có: x12 + x22 + 2(x1x2)2 = 7x1x2
\(\Leftrightarrow\) (x1 + x2)2 - 2x1x2 + 2(x1x2)2 = 7x1x2 (*)
Thay (I) vào (*) ta được:
(-2)2 - 2(m - 3) + 2(m - 3)2 = 7(m - 3)
\(\Leftrightarrow\) 4 - 9m + 27 + 2(m2 - 6m + 9) = 0
\(\Leftrightarrow\) 31 - 9m + 2m2 - 12m + 18 = 0
\(\Leftrightarrow\) 2m2 - 21m + 49 = 0
\(\Leftrightarrow\) \(\left[{}\begin{matrix}m=7\\m=3,5\end{matrix}\right.\)
Vậy ...
Chúc bn học tốt!