Nghiệm của phương trình:
(2x-3)2-4x2-297=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



![]()
![]()
Xét hàm ![]() trên
trên ![]()

Phương trình đã cho có bốn nghiệm phân biệt khi và chỉ khi phương trình (*) có hai nghiệm phân biệt lớn hơn 1 và khác ![]()
Chọn A.

Δ=(2m-1)^2-4*2*(m-1)
=4m^2-4m+1-8m+8
=4m^2-12m+9=(2m-3)^2>=0
=>PT luôn có 2 nghiệm
4x1^2+4x2^2+2x1x2=0
=>4[(x1+x2)^2-2x1x2]+m-1=0
=>4[(-2m+1)^2/4-2*(m-1)/2]+m-1=0
=>(2m-1)^2-4(m-1)+m-1=0
=>4m^2-4m+1-3m+3=0
=>4m^2-7m+4=0
=>\(m\in\varnothing\)

Phương trình 4x2 + 2x – 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x1; x2
Theo hệ thức Vi-et ta có: 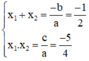

a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: 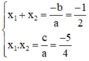
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: 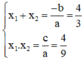
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: 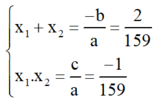

A=(x1-x2)^2-x1^2+x1(x1+x2)
=(x1-x2)^2+x1x2
=(x1+x2)^2-x1x2
=(1/2)^2-(-1/4)=1/4+1/4=1/2

Đáp án B



Ta có bảng biến thiên
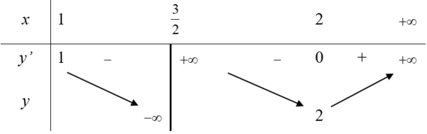
Phương trình (1) có bốn nghiệm phân biệt
⇔ * có hai nghiệm phân biệt lớn hơn 1
Mà m nguyên và m ∈ − 2019 ; 2019 nên ta có m ∈ 3 ; 4 ; ... ; 2018 .
Vậy có 2016 giá trị m thỏa mãn bài toán.
\(\left(2x-3\right)^2-4x^2-297=0\)
\(\Rightarrow\left(2x-3-2x\right)\left(2x-3+2x\right)=297\)
\(\Rightarrow-3\left(4x-3\right)=297\)
\(\Rightarrow4x-3=-99\)
\(\Rightarrow x=-24\)
=4x2 -12x +9 -4x2 - 297 =0
-12x -288=0
x = 288/12= 24
x = 24